Оглавление
| Введение
| П1
| П2
| П3
| Литература
Лекции:
1,
2-3,
4-6,
7.1,
7.2,
8,
9,
10,
11.1,
11.2-12,
13-14,
15-16
Лекция 10. Оценка и интерпретатор ответа
Эта глава посвящена обзору различных видов оценок, способам их вычисления. В ней так же рассмотрен способ определения уровня уверенности сети в выданном ответе и приведен способ построения оценок, позволяющих определять уровень уверенности. Приведен основной принцип проектирования оценки – надо учить сеть тому, что мы хотим от нее получить.
Основные функции, которые должна выполнять оценка:
- Вычислять оценку решения, выданного сетью.
- Вычислять производные этой оценки по выходным сигналам сети.
Кроме оценок, в первом разделе этой главы рассмотрен другой, тесно связанный с ней объект – интерпретатор ответа. Основное назначение этого объекта – интерпретировать выходной вектор сети как ответ, понятный пользователю. Однако, при определенном построении интерпретатора и правильно построенной по нему оценке, интерпретатор ответа может также оценивать уровень уверенности сети в выданном ответе.
При частичной аппаратной реализации нейрокомпьютера включение функции оценки в аппаратную часть не эффективно, поскольку оценка является сложным устройством (многие функции оценки включают в себя операции сортировки, и другие аналогичные операции). Однако при аппаратной реализации обученной нейронной сети (даже если предусматривается доучивание сети) аппаратная реализация интерпретатора ответа может оказаться эффективной, поскольку для обученной сети интерпретатор уже не меняется, и по сравнению с оценкой интерпретатор ответа достаточно прост.
Интерпретатор ответа
Как было показано в главе «Описание нейронных сетей», ответ, выдаваемый нейронной сетью, как правило, является числом, из диапазона [a,b]. Если ответ выдается несколькими нейронами, то на выходе сети мы имеем вектор, каждый компонент которого лежит в интервале [a,b]. Если в качестве ответа требуется число из этого диапазона, то мы можем его получить. Однако, в большинстве случаев это не так. Достаточно часто требуемая в качестве ответа величина лежит в другом диапазоне. Например, при предсказании температуры воздуха 25 июня в Красноярске ответ должен лежать в интервале от 5 до 35 градусов Цельсия. Сеть не может дать на выходе такого сигнала. Значит, прежде чем обучать сеть необходимо решить в каком виде будем требовать ответ. В данном случае ответ можно требовать в виде 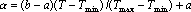 , где T – требуемая температура, , где T – требуемая температура, 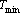 и и 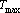 – минимальная и максимальная температуры, a – ответ, который будем требовать от сети. При интерпретации ответа необходимо проделать обратное преобразование. Если сеть выдала сигнал a, то ответом является величина – минимальная и максимальная температуры, a – ответ, который будем требовать от сети. При интерпретации ответа необходимо проделать обратное преобразование. Если сеть выдала сигнал a, то ответом является величина 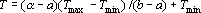 . Таким образом, можно интерпретировать выдаваемый сетью сигнал, как величину из любого, наперед заданного диапазона. . Таким образом, можно интерпретировать выдаваемый сетью сигнал, как величину из любого, наперед заданного диапазона.
Если при составлении обучающего множества ответ на примеры определялся с некоторой погрешностью, то от сети следует требовать не точного воспроизведения ответа, а попадания в интервал заданной ширины. В этом случае интерпретатор ответа может выдать сообщение о правильности (попадании в интервал) ответа.
Другим, часто встречающимся случаем, является предсказание сетью принадлежности входного вектора одному из заданных классов. Такие задачи называют задачами классификации, а решающие их сети – классификаторами. В простейшем случае задача классификации ставится следующим образом: пусть задано N классов. Тогда нейросеть выдает вектор из N сигналов. Однако, нет единого универсального правила интерпретации этого вектора. Наиболее часто используется интерпретация по максимуму: номер нейрона, выдавшего максимальный по величине сигнал, является номером класса, к которому относится предъявленный сети входной вектор. Такие интерпретаторы ответа называются интерпретаторами, кодирующими ответ номером канала (номер нейрона – номер класса). Все интерпретаторы, использующие кодирование номером канала, имеют один большой недостаток – для классификации на N классов требуется N выходных нейронов. При большом N требуется много выходных нейронов для получения ответа. Однако существуют и другие виды интерпретаторов.
Двоичный интерпретатор. Основная идея двоичного интерпретатора – получение на выходе нейронной сети двоичного кода номера класса. Это достигается двухэтапной интерпретацией:
- Каждый выходной сигнал нейронной сети интерпретируется как 1, если он больше (a+b)/2, и как 0 в противном случае.
- Полученная последовательность нулей и единиц интерпретируется как двоичное число.
Двоичный интерпретатор позволяет интерпретировать N выходных сигналов нейронной сети как номер одного из 2N классов.
Порядковый интерпретатор. Порядковый интерпретатор кодирует номер класса подстановкой. Отсортируем вектор выходных сигналов по возрастанию. Вектор, составленный из номеров нейронов последовательно расположенных в отсортированном векторе выходных сигналов, будет подстановкой. Если каждой подстановке приписать номер класса, то такой интерпретатор может закодировать N! классов используя N выходных сигналов.
Уровень уверенности
Часто при решении задач классификации с использованием нейронных сетей недостаточно простого ответа «входной вектор принадлежит K-му классу». Хотелось бы также оценить уровень уверенности в этом ответе. Для различных интерпретаторов вопрос определения уровня уверенности решается по-разному. Однако, необходимо учесть, что от нейронной сети нельзя требовать больше того, чему ее обучили. В этом разделе будет рассмотрен вопрос об определении уровня уверенности для нескольких интерпретаторов, а в следующем будет показано, как построить оценку так, чтобы нейронная сеть позволяла его определить.
1. Кодирование номером канала. Знаковый интерпретатор. Знаковый интерпретатор работает в два этапа.
- Каждый выходной сигнал нейронной сети интерпретируется как 1, если он больше (a+b)/2, и как 0 в противном случае.
- Если в полученном векторе только одна единица, то номером класса считается номер нейрона, сигнал которого интерпретирован как 1. В противном случае ответом считается неопределенный номер класса (ответ «не знаю»).
Для того чтобы ввести уровень уверенности для этого интерпретатора потребуем, чтобы при обучении сети для всех примеров было верно неравенство: 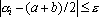 , где , где 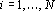 ; ; 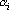 - i-ый выходной сигнал. e – уровень надежности (насколько сильно сигналы должны быть отделены от (a+b)/2 при обучении). В этом случае уровень уверенности R определяется следующим образом: - i-ый выходной сигнал. e – уровень надежности (насколько сильно сигналы должны быть отделены от (a+b)/2 при обучении). В этом случае уровень уверенности R определяется следующим образом: 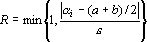 . Таким образом, при определенном ответе уровень уверенности показывает, насколько ответ далек от неопределенного, а в случае неопределенного ответа – насколько он далек от определенного. . Таким образом, при определенном ответе уровень уверенности показывает, насколько ответ далек от неопределенного, а в случае неопределенного ответа – насколько он далек от определенного.
2. Кодирование номером канала. Максимальный интерпретатор. Максимальный интерпретатор в качестве номера класса выдает номер нейрона, выдавшего максимальный сигнал. Для такого интерпретатора в качестве уровня уверенности естественно использовать некоторую функцию от разности между максимальным и вторым по величине сигналами. Для этого потребуем, чтобы при обучении для всех примеров обучающего множества разность между максимальным и вторым по величине сигналами была не меньше уровня надежности e. В этом случае уровень уверенности вычисляется по следующей формуле: 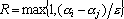 , где , где 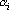 – максимальный, а – максимальный, а 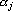 – второй по величине сигналы. – второй по величине сигналы.
3. Двоичный интерпретатор. Уровень надежности для двоичного интерпретатора вводится так же, как и для знакового интерпретатора при кодировании номером канала.
4. Порядковый интерпретатор. При использовании порядкового интерпретатора в качестве уровня уверенности естественно брать функцию от разности двух соседних сигналов в упорядоченном по возрастанию векторе выходных сигналов. Для этого потребуем, чтобы при обучении для всех примеров обучающего множества в упорядоченном по возрастанию векторе выходных сигналов разность между двумя соседними элементами была не меньше уровня надежности e. В этом случае уровень уверенности можно вычислить по формуле 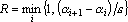 , причем вектор выходных сигналов предполагается отсортированным по возрастанию. , причем вектор выходных сигналов предполагается отсортированным по возрастанию.
В заключение заметим, что для ответа типа число, ввести уровень уверенности подобным образом невозможно. Пожалуй, единственным способом оценки достоверности результата является консилиум нескольких сетей – если несколько сетей обучены решению одной и той же задачи, то в качестве ответа можно выбрать среднее значение, а по отклонению ответов от среднего можно оценить достоверность результата.
Построение оценки по интерпретатору
Если в качестве ответа нейронная сеть должна выдать число, то естественной оценкой является квадрат разности выданного сетью выходного сигнала и правильного ответа. Все остальные оценки для обучения сетей решению таких задач являются модификациями данной. Приведем пример такой модификации. Пусть при составлении задачника величина  , являющаяся ответом, измерялась с некоторой точностью e. Тогда нет смысла требовать от сети обучиться выдавать в качестве ответа именно величину , являющаяся ответом, измерялась с некоторой точностью e. Тогда нет смысла требовать от сети обучиться выдавать в качестве ответа именно величину  . Достаточно, если выданный сетью ответ попадет в интервал . Достаточно, если выданный сетью ответ попадет в интервал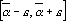 . Оценка, удовлетворяющая этому требованию, имеет вид: . Оценка, удовлетворяющая этому требованию, имеет вид:
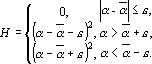
Эту оценку будем называть оценкой числа с допуском e.
Для задач классификации также можно пользоваться оценкой типа суммы квадратов отклонений выходных сигналов сети от требуемых ответов. Однако, эта оценка плоха тем, что, во-первых, требования при обучении сети не совпадают с требованиями интерпретатора, во-вторых, такая оценка не позволяет оценить уровень уверенности сети в выданном ответе. Достоинством такой оценки является ее универсальность. Опыт работы с нейронными сетями, накопленный красноярской группой НейроКомп, свидетельствует о том, что при использовании оценки, построенной по интерпретатору, в несколько раз возрастает скорость обучения.
Для оценок, построенных по интерпретатору потребуется следующая функция оценки
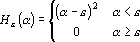
и ее производная
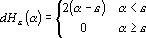 . .
Рассмотрим построение оценок по интерпретатору для четырех рассмотренных в предыдущем разделе интерпретаторов ответа.
1. Кодирование номером канала. Знаковый интерпретатор. Пусть для рассматриваемого примера правильным ответом является k-ый класс. Тогда вектор выходных сигналов сети должен удовлетворять следующей системе неравенств:
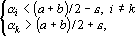
где e- уровень надежности.
Оценку, вычисляющую расстояние от точки a в пространстве выходных сигналов до множества точек, удовлетворяющих этой системе неравенств, можно записать в виде:
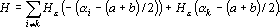
Производная оценки по i-му выходному сигналу равна
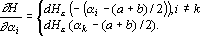 . .
2. Кодирование номером канала. Максимальный интерпретатор. Пусть для рассматриваемого примера правильным ответом является k-ый класс. Тогда вектор выходных сигналов сети должен удовлетворять следующей системе неравенств: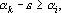 при при 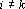 . Оценкой решения сетью данного примера является расстояние от точки a в пространстве выходных сигналов до множества точек, удовлетворяющих этой системе неравенств. Для записи оценки, исключим из вектора выходных сигналов сигнал . Оценкой решения сетью данного примера является расстояние от точки a в пространстве выходных сигналов до множества точек, удовлетворяющих этой системе неравенств. Для записи оценки, исключим из вектора выходных сигналов сигнал 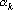 , а остальные сигналы отсортируем по убыванию. Обозначим величину , а остальные сигналы отсортируем по убыванию. Обозначим величину  через через 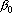 , а вектор отсортированных сигналов через , а вектор отсортированных сигналов через 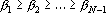 . Система неравенств в этом случае приобретает вид . Система неравенств в этом случае приобретает вид 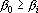 , при i>1. Множество точек удовлетворяющих этой системе неравенств обозначим через D. Очевидно, что если , при i>1. Множество точек удовлетворяющих этой системе неравенств обозначим через D. Очевидно, что если 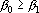 , то точка b принадлежит множеству D. Если , то точка b принадлежит множеству D. Если 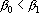 , то найдем проекцию точки b на гиперплоскость , то найдем проекцию точки b на гиперплоскость 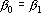 . Эта точка имеет координаты . Эта точка имеет координаты 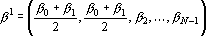 . Если . Если 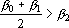 , то точка , то точка 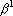 принадлежит множеству D. Если нет, то точку b нужно проектировать на гиперплоскость принадлежит множеству D. Если нет, то точку b нужно проектировать на гиперплоскость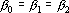 . Найдем эту точку. Ее координаты можно записать в следующем виде . Найдем эту точку. Ее координаты можно записать в следующем виде 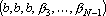 . Эта точка обладает тем свойством, что расстояние от нее до точки b минимально. Таким образом, для нахождения величины b достаточно взять производную от расстояния по b и приравнять ее к нулю: . Эта точка обладает тем свойством, что расстояние от нее до точки b минимально. Таким образом, для нахождения величины b достаточно взять производную от расстояния по b и приравнять ее к нулю:
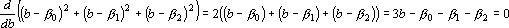
Из этого уравнения находим b и записываем координаты точки 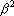 : :
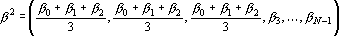 . .
Эта процедура продолжается дальше, до тех пор, пока при некотором l не выполнится неравенство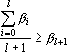 или пока l не окажется равной N-1. Оценкой является расстояние от точки b до точки или пока l не окажется равной N-1. Оценкой является расстояние от точки b до точки 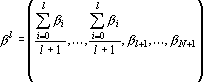 . Она равна следующей величине . Она равна следующей величине 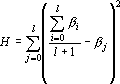 . .
Производная оценки по выходному сигналу 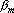 равна равна
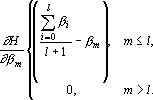
Для перехода к производным по исходным выходным сигналам 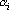 необходимо обратить сделанные на первом этапе вычисления оценки преобразования. необходимо обратить сделанные на первом этапе вычисления оценки преобразования.
3. Двоичный интерпретатор. Оценка для двоичного интерпретатора строится точно также как и для знакового интерпретатора при кодировании номером канала. Пусть правильным ответом является k-ый класс, тогда обозначим через K множество номеров сигналов, которым в двоичном представлении k соответствуют единицы. При уровне надежности оценка задается формулой:

Производная оценки по i-му выходному сигналу равна:
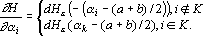 . .
4. Порядковый интерпретатор. Для построения оценки по порядковому интерпретатору необходимо предварительно переставить компоненты вектора a в соответствии с подстановкой, кодирующей правильный ответ. Обозначим полученный в результате вектор через 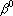 . Множество точек, удовлетворяющих условию задачи, описывается системой уравнений . Множество точек, удовлетворяющих условию задачи, описывается системой уравнений 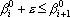 , где e – уровень надежности. Обозначим это множество через D. Оценка задается расстоянием от точки b до проекции этой точки на множество D. Опишем процедуру вычисления проекции. , где e – уровень надежности. Обозначим это множество через D. Оценка задается расстоянием от точки b до проекции этой точки на множество D. Опишем процедуру вычисления проекции.
- Просмотрев координаты точки
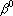 , отметим те номера координат, для которых нарушается неравенство , отметим те номера координат, для которых нарушается неравенство 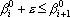 . .
- Множество отмеченных координат либо состоит из одной последовательности последовательных номеров
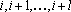 , или из нескольких таких последовательностей. Найдем точку , или из нескольких таких последовательностей. Найдем точку 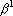 , которая являлась бы проекцией точки , которая являлась бы проекцией точки 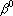 на гиперплоскость, определяемую уравнениями на гиперплоскость, определяемую уравнениями 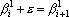 , где i пробегает множество индексов отмеченных координат. Пусть множество отмеченных координат распадается на n последовательностей, каждая из которых имеет вид , где i пробегает множество индексов отмеченных координат. Пусть множество отмеченных координат распадается на n последовательностей, каждая из которых имеет вид 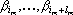 , где m – номер последовательности. Тогда точка , где m – номер последовательности. Тогда точка 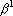 имеет вид: имеет вид:
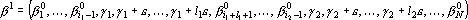
- Точка
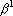 является проекцией, и следовательно, расстояние от является проекцией, и следовательно, расстояние от 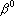 до до 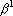 должно быть минимальным. Это расстояние равно должно быть минимальным. Это расстояние равно 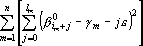 . Для нахождения минимума этой функции необходимо приравнять к нулю ее производные по . Для нахождения минимума этой функции необходимо приравнять к нулю ее производные по 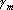 . Получаем систему уравнений . Получаем систему уравнений 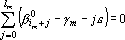 . Решая ее, находим . Решая ее, находим 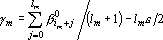 . .
- Если точка
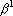 удовлетворяет неравенствам, приведенным в первом пункте процедуры, то расстояние от нее до точки удовлетворяет неравенствам, приведенным в первом пункте процедуры, то расстояние от нее до точки 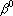 является оценкой. В противном случае, повторяем первый шаг процедуры, используя точку является оценкой. В противном случае, повторяем первый шаг процедуры, используя точку 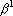 вместо вместо 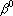 ; Объединяем полученный список отмеченных компонентов со списком, полученным при поиске предыдущей точки; находим точку ; Объединяем полученный список отмеченных компонентов со списком, полученным при поиске предыдущей точки; находим точку 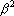 , повторяя все шаги процедуры, начиная со второго. , повторяя все шаги процедуры, начиная со второго.
Отметим, что в ходе процедуры число отмеченных последовательностей соседних индексов не возрастает. Некоторые последовательности могут сливаться, но новые возникать не могут. После нахождения проекции можно записать оценку:
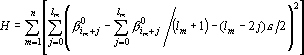 . .
Обозначим через 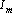 m-ую последовательность соседних координат, выделенную при последнем исполнении первого шага процедуры вычисления оценки: m-ую последовательность соседних координат, выделенную при последнем исполнении первого шага процедуры вычисления оценки: 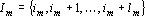 . Тогда производную оценки по выходному сигналу . Тогда производную оценки по выходному сигналу 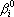 можно записать в следующем виде: можно записать в следующем виде:
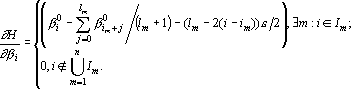
Таким образом, построение оценки по интерпретатору сводится к следующей процедуре.
- Определяем множество допустимых точек, то есть таких точек в пространстве выходных сигналов, которые интерпретатор ответа будет интерпретировать как правильный ответ со стопроцентным уровнем уверенности.
- Находим проекцию выданной сетью точки на это множество. Проекцией является ближайшая точка из множества.
- Записываем оценку как расстояние от точки, выданной сетью, до ее проекции на множество допустимых точек.
Оценка обучающего множества. Вес примера
В предыдущем разделе был рассмотрен ряд оценок, позволяющих оценить решение сетью конкретного примера. Однако, ситуация, когда сеть хотят обучить решению только одного примера, достаточно редка. Обычно сеть должна научиться решать все примеры обучающего множества. Ряд алгоритмов обучения, которые будут рассматриваться в главе «Учитель», требуют возможности обучать сеть решению всех примеров одновременно и, соответственно, оценивать решение сетью всех примеров обучающего множества. Как уже отмечалось, обучение нейронной сети – это процесс минимизации в пространстве обучаемых параметров функции оценки. Большинство алгоритмов обучения используют способность нейронных сетей быстро вычислять вектор градиента функции оценки по обучаемым параметрам. Обозначим оценку отдельного примера через 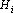 . а оценку всего обучающего множества через . а оценку всего обучающего множества через 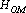 . Простейший способ получения . Простейший способ получения 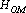 из из 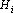 – простая сумма. При этом вектор градиента вычисляется очень просто: – простая сумма. При этом вектор градиента вычисляется очень просто:
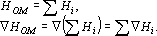 . .
Таким образом, используя способность сети вычислять градиент функции оценки решения одного примера, можно получить градиент функции оценки всего обучающего множества.
Обучение по всему обучающему множеству позволяет задействовать дополнительные механизмы ускорения обучения. Большинство этих механизмов будет рассмотрено в главе «Учитель». В этом разделе будет рассмотрен только один из них – использование весов примеров. Использование весов примеров может быть вызвано одной из следующих причин.
- Один из примеров плохо обучается.
- Число примеров разных классов в обучающем множестве сильно отличаются друг от друга.
- Примеры в обучающем множестве имеют различную достоверность.
Рассмотрим первую причину – пример плохо обучается. Под «плохо обучается» будем понимать медленное снижение оценки данного примера по отношению к снижению оценки по обучающему множеству. Для того чтобы ускорить обучение данного примера, ему можно приписать вес, больший, чем у остальных примеров. При этом оценка по обучающему множеству и ее градиент можно записать в следующем виде: 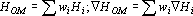 . где . где 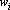 – вес i-го примера. Эту функцию оценки будем называть оценкой взвешенных примеров. При этом градиент, вычисленный по оценке решения сетью этого примера, войдет в суммарный градиент с большим весом, и, следовательно, сильнее повлияет на выбор направления обучения. Этот способ применим также и для коррекции проблем, связанных со второй причиной – разное число примеров разных классов. Однако в этом случае увеличиваются веса всем примерам того класса, в котором меньше примеров. Опыт показывает, что использование весов в таких ситуациях позволяет улучшить обобщающие способности сетей. – вес i-го примера. Эту функцию оценки будем называть оценкой взвешенных примеров. При этом градиент, вычисленный по оценке решения сетью этого примера, войдет в суммарный градиент с большим весом, и, следовательно, сильнее повлияет на выбор направления обучения. Этот способ применим также и для коррекции проблем, связанных со второй причиной – разное число примеров разных классов. Однако в этом случае увеличиваются веса всем примерам того класса, в котором меньше примеров. Опыт показывает, что использование весов в таких ситуациях позволяет улучшить обобщающие способности сетей.
В случае различной достоверности примеров в обучающем множестве функция взвешенных примеров не применима. Действительно, если известно, что достоверность ответа в k-ом примере в два раза ниже, чем в l-ом, хотелось бы, чтобы обученная сеть выдавала для k-ого примера в два раза меньший уровень уверенности. Этого можно достичь, если при вычислении оценки k-ого примера будет использоваться в два раза меньший уровень надежности. Оценка обучающего множества в этом случае вычисляется по формуле без весов, а достоверность учитывается непосредственно при вычислении оценки по примеру. Такую оценку будем называть оценкой взвешенной достоверности.
Таким образом, каждый пример может иметь два веса: вес примера и достоверность примера. Кроме того, при решении задач классификации каждый класс может обладать собственным весом. Окончательно функцию оценки по обучающему множеству и ее градиент можно записать в следующем виде:
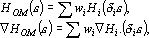
где 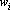 – вес примера, – вес примера, 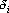 – его достоверность. – его достоверность.
Глобальные и локальные оценки
В предыдущих разделах был рассмотрен ряд оценок. Эти оценки обладают одним общим свойством – для вычисления оценки по примеру, предъявленному сети, достаточно знать выходной вектор, выданный сетью при решении этого примера, и правильный ответ. Такие оценки будем называть локальными. Приведем точное определение.
Определение. Локальной называется любая оценка, являющаяся линейной комбинацией произвольных непрерывно дифференцируемых функций, каждая из которых зависит от оценки только одного примера.
Использование локальных оценок позволяет обучать сеть решению как отдельно взятого примера, так и всего обучающего множества в целом. Однако существуют задачи, для которых невозможно построить локальную оценку. Более того, для некоторых задач нельзя построить даже обучающее множество. Использование нелокальных оценок возможно даже при решении задач классификации.
Приведем два примера нелокальных оценки.
Кинетическая оценка для задачи классификации. Пусть в обучающее множество входят примеры k классов. Требуется обучить сеть так, чтобы в пространстве выходных сигналов множества примеров разных классов были попарно линейно разделимы.
Пусть сеть выдает N выходных сигналов. Для решения задачи достаточно, чтобы в ходе обучения все точки в пространстве выходных сигналов, соответствующие примерам одного класса, собирались вокруг одной точки – центра концентрации класса, и чтобы центры концентрации разных классов были как можно дальше друг от друга. В качестве центра концентрации можно выбрать барицентр множества точек, соответствующих примерам данного класса.
Таким образом, функция оценки должна состоять из двух компонентов: первая реализует притяжение между примерами одного класса и барицентром этого класса, а вторая отвечает за отталкивание барицентров разных классов. Обозначим точку в пространстве выходных сигналов, соответствующую m-му примеру, через 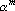 , множество примеров i-го класса через , множество примеров i-го класса через 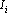 , барицентр точек, соответствующих примерам этого класса, через , барицентр точек, соответствующих примерам этого класса, через 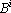 ( (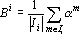 ), число примеров в i-ом классе через ), число примеров в i-ом классе через  , а расстояние между точками a и b через , а расстояние между точками a и b через 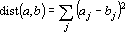 . Используя эти обозначения, можно записать притягивающий компонент функции оценки для всех примеров i-го класса в виде: . Используя эти обозначения, можно записать притягивающий компонент функции оценки для всех примеров i-го класса в виде:
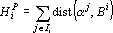
Функция оценки 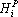 обеспечивает сильное притяжение для примеров, находящихся далеко от барицентра. Притяжение ослабевает с приближением к барицентру. Компонент функции оценки, отвечающий за отталкивание барицентров разных классов, должен обеспечивать сильное отталкивание близких барицентров и ослабевать с удалением барицентров друг от друга. Такими свойствами обладает гравитационное отталкивание. Используя гравитационное отталкивание можно записать второй компонент функции оценки в виде: обеспечивает сильное притяжение для примеров, находящихся далеко от барицентра. Притяжение ослабевает с приближением к барицентру. Компонент функции оценки, отвечающий за отталкивание барицентров разных классов, должен обеспечивать сильное отталкивание близких барицентров и ослабевать с удалением барицентров друг от друга. Такими свойствами обладает гравитационное отталкивание. Используя гравитационное отталкивание можно записать второй компонент функции оценки в виде: 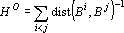 . Таким образом, оценку, обеспечивающую сближение точек, соответствующих примерам одного класса, и отталкивание барицентров, можно записать в виде: . Таким образом, оценку, обеспечивающую сближение точек, соответствующих примерам одного класса, и отталкивание барицентров, можно записать в виде:
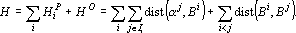
Вычислим производную оценки по j-му выходному сигналу, полученному при решении i-го примера. Пусть i-ый пример принадлежит l-му классу. Тогда производная имеет вид:
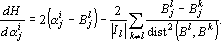
Эту оценку будем называть кинетической. Существует одно основное отличие этой оценки от всех других, ранее рассмотренных, оценок для решения задач классификации. При использовании традиционных подходов, сначала выбирают интерпретатор ответа, затем строят по выбранному интерпретатору функцию оценки, и только затем приступают к обучению сети. Для кинетической оценки такой подход не применим. Действительно, до того как будет закончено обучение сети невозможно построить интерпретатор. Кроме того, использование кинетической оценки, делает необходимым обучение сети решению всех примеров обучающего множества одновременно. Это связанно с невозможностью вычислить оценку одного примера. Кинетическая оценка, очевидно, не является локальной: для вычисления производных оценки по выходным сигналам примера необходимо знать барицентры всех классов, для вычисления которых, в свою очередь, необходимо знать выходные сигналы, получаемые при решении всех примеров обучающего множества.
Интерпретатор для кинетической оценки строится следующим образом. Для построения разделителя i-го и j-го классов строим плоскость, перпендикулярную к вектору 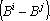 Уравнение этой плоскости можно записать в виде Уравнение этой плоскости можно записать в виде
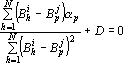 . .
Для определения константы D находим среди точек i-го класса ближайшую к барицентру j-го класса. Подставляя координаты этой точки в уравнение гиперплоскости, получаем уравнение на D. Решив это уравнение, находим величину 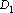 . Используя ближайшую к барицентру i-го класса точку j-го класса, находим величину . Используя ближайшую к барицентру i-го класса точку j-го класса, находим величину 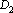 . Искомая константа D находится как среднее арифметическое между . Искомая константа D находится как среднее арифметическое между 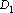 и и 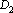 . Для отнесения произвольного вектора к i-му или j-му классу достаточно подставить его значения в левую часть уравнения разделяющей гиперплоскости. Если значение левой части уравнения получается больше нуля, то вектор относится к j-му классу, в противном случае – к i-му. . Для отнесения произвольного вектора к i-му или j-му классу достаточно подставить его значения в левую часть уравнения разделяющей гиперплоскости. Если значение левой части уравнения получается больше нуля, то вектор относится к j-му классу, в противном случае – к i-му.
Интерпретатор работает следующим образом: если для i-го класса все разделители этого класса с остальными классами выдали ответ i-ый класс, то окончательным ответом является i-ый класс. Если такого класса не нашлось, то ответ «не знаю». Ситуация, когда для двух различных классов все разделители подтвердили принадлежность к этому классу, невозможна, так как разделитель этих двух классов должен был отдать предпочтение одному из них.
Рассмотренный пример решения задачи с использованием нелокальной оценки позволяет выделить основные черты обучения с нелокальной оценкой:
- Невозможность оценить решение одного примера.
- Невозможность оценить правильность решения примера до окончания обучения.
- Невозможность построения интерпретатора ответа до окончания обучения.
Этот пример является отчасти надуманным, поскольку его можно решить с использованием более простых локальных оценок. Ниже приведен пример задачи, которую невозможно решить с использованием локальных оценок.
Генератор случайных чисел. Необходимо обучить сеть генерировать последовательность случайных чисел из диапазона [0,1]с заданными k первыми моментами. Напомним, что для выборки роль первого момента играет среднее значение, второго – средний квадрат, третьего – средний куб и так далее. Есть два пути решения этой задачи. Первый – используя стандартный генератор случайных чисел подготовить задачник и обучить по нему сеть. Этот путь плох тем, что такой генератор будет просто воспроизводить последовательность чисел, записанную в задачнике. Для получения такого результата можно просто хранить задачник.
Второй вариант – обучать сеть без задачника! Пусть нейросеть принимает один входной сигнал и выдает один выходной. При использовании сети выходной сигнал первого срабатывания сети (первое случайное число) будет служить входным сигналом для второго срабатывания сети и так далее.
Для построения оценки зададимся тремя наборами чисел: 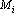 – необходимое значение i-го момента, – необходимое значение i-го момента,  – длина последовательности, на которой i-ый момент сгенерированной последовательности должен не более чем на – длина последовательности, на которой i-ый момент сгенерированной последовательности должен не более чем на  отличаться от отличаться от 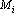 . .  – точность вычисления i-го момента. – точность вычисления i-го момента.
Выборочная оценка совпадения i-го момента в сгенерированной последовательности на отрезке, начинающемся с j-го случайного числа, вычисляется по следующей формуле: 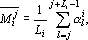 где где 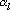 – выходной сигнал, полученный на l-ом срабатывании сети. Для оценки точности совпадения i-го момента в сгенерированной последовательности на отрезке, начинающемся с j-го случайного числа, воспользуемся оценкой числа с допуском – выходной сигнал, полученный на l-ом срабатывании сети. Для оценки точности совпадения i-го момента в сгенерированной последовательности на отрезке, начинающемся с j-го случайного числа, воспользуемся оценкой числа с допуском  : :
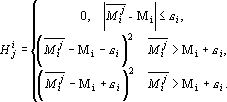
Таким образом, при обучении сети генерации последовательности из N случайных чисел оценку можно записать в следующем виде:
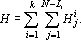
Производная оценки по выходному сигналу l-го срабатывания сети можно записать в следующем виде:
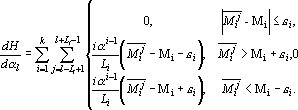
Используя эту оценку можно обучать сеть генерировать случайные числа. Удобство этого подхода к решению задачи обучения генератора случайных чисел в том, что можно достаточно часто менять инициирующий сеть входной сигнал, что позволит сети генерировать не одну, а много различных последовательностей, обладающих всеми необходимыми свойствами.
При использовании предложенной оценки нет никаких гарантий того, что в генерируемой сетью последовательности не появятся сильно скоррелированные подпоследовательности. Для удаления корреляций можно модифицировать оценку так, чтобы она возрастала при появлении корреляций. Рассмотрим две подпоследовательности длинны L, первая из которых начинается с 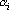 , а другая с , а другая с 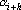 . Коэффициент корреляции этих последовательностей записывается в виде: . Коэффициент корреляции этих последовательностей записывается в виде:
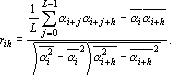
В этой формуле приняты следующие обозначения: 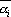 - среднее по последовательности, начинающейся с - среднее по последовательности, начинающейся с 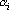 ; ; 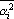 – средний квадрат последовательности начинающейся с – средний квадрат последовательности начинающейся с 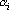 . Вычисление такого коэффициента корреляции довольно долгий процесс. Однако вместо выборочных моментов в формулу можно подставить значения моментов, которые последовательность должна иметь. В этом случае формула сильно упрощается: . Вычисление такого коэффициента корреляции довольно долгий процесс. Однако вместо выборочных моментов в формулу можно подставить значения моментов, которые последовательность должна иметь. В этом случае формула сильно упрощается:
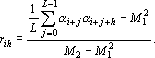
Добавку для удаления корреляций последовательностей длиной от 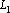 до до  и смещенных друг относительно друга на смещения от и смещенных друг относительно друга на смещения от 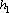 до до 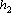 можно записать в виде: можно записать в виде:
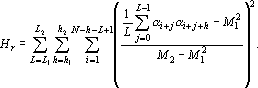
При необходимости можно ввести и другие поправки, учитывающие требования к генератору случайных чисел.
Составные интерпретатор ответа и оценка
При использовании нейронных сетей для решения различных задач возникает необходимость получать от сети не один ответ, а несколько. Например, при обучении сети решению задачи диагностики отклонений в реакции на стресс нейронная сеть должна была определить наличие или отсутствие тринадцати различных патологий. Если одна сеть может выдавать только один ответ, то для решения задачи необходимо задействовать тринадцать сетей. Однако в этом нет необходимости. Поскольку каждый ответ, который должна выдавать сеть, имеет только два варианта, то можно использовать для его получения классификатор на два класса. Для такого классификатора необходимо два выходных сигнала. Тогда для решения задачи достаточно получать 26 выходных сигналов: первые два сигнала – для определения первой патологии, третий и четвертый – для второй и так далее. Таким образом, интерпретатор ответа для этой задачи состоит из тринадцати интерпретаторов, а оценка из тринадцати оценок. Более того, нет никаких ограничений на типы используемых интерпретаторов или оценок. Возможна комбинация, например, следующих ответов: число с допуском, классификатор на восемь классов, случайное число.
При использовании таких составных оценок и интерпретаторов каждый из этих компонентов должен следить за тем, чтобы каждая частная оценка или интерпретатор получали на вход те данные, которые им необходимы.
Оглавление
| Введение
| П1
| П2
| П3
| Литература
Лекции:
1,
2-3,
4-6,
7.1,
7.2,
8,
9,
10,
11.1,
11.2-12,
13-14,
15-16
|