Оглавление
| Введение
| П1
| П2
| П3
| Литература
Лекции:
1,
2-3,
4-6,
7.1,
7.2,
8,
9,
10,
11.1,
11.2-12,
13-14,
15-16
Лекции 4, 5 и 6. Нейронные сети ассоциативной памяти, функционирующие в дискретном времени
Нейронные сети ассоциативной памяти – сети восстанавливающие по искаженному и/или зашумленному образу ближайший к нему эталонный. Исследована информационная емкость сетей и предложено несколько путей ее повышения, в том числе – ортогональные тензорные (многочастичные) сети. Описаны способы предобработки, позволяющие конструировать нейронные сети ассоциативной памяти для обработки образов, инвариантной относительно групп преобразований. Описан численный эксперимент по использованию нейронных сетей для декодирования различных кодов. Доказана теорема об информационной емкости тензорных сетей.
Описание задачи
Прежде чем заниматься конструированием сетей ассоциативной памяти необходимо ответить на следующие два вопроса: «Как устроена ассоциативная память?» и «Какие задачи она решает?». Когда мы задаем эти вопросы, имеется в виду не устройство отделов мозга, отвечающих за ассоциативную память, а наше представление о макропроцессах, происходящих при проявлении ассоциативной памяти.
Принято говорить, что у человека возникла ассоциация, если при получении некоторой неполной информации он может подробно описать объект, к которому по его мнению относится эта информация. Достаточно хорошим примером может служить описание малознакомого человека. К примеру, при высказывании: «Слушай, а что за парень, с которым ты вчера разговаривал на вечеринке, такой высокий блондин?»– у собеседника возникает образ вчерашнего собеседника, не ограничивающийся ростом и цветом волос. В ответ на заданный вопрос он может рассказать об этом человеке довольно много. При этом следует заметить, что содержащейся в вопросе информации явно недостаточно для точной идентификации собеседника. Более того, если вчерашний собеседник был случайным, то без дополнительной информации его и не вспомнят.
Подводя итог описанию можно сказать, что ассоциативная память позволяет по неполной и даже частично недостоверной информации восстановить достаточно полное описание знакомого объекта. Слово знакомого является очень важным, поскольку невозможно вызвать ассоциации с незнакомыми объектами. При этом объект должен быть знаком тому, у кого возникают ассоциации.
Одновременно рассмотренные примеры позволяют сформулировать решаемые ассоциативной памятью задачи:
- Соотнести входную информацию со знакомыми объектами, и дополнить ее до точного описания объекта.
- Отфильтровать из входной информации недостоверную, а на основании оставшейся решить первую задачу.
Очевидно, что под точным описанием объекта следует понимать всю информацию, которая доступна ассоциативной памяти. Вторая задача решается не поэтапно, а одновременно происходит соотнесение полученной информации с известными образцами и отсев недостоверной информации.
Нейронным сетям ассоциативной памяти посвящено множество работ (см. например, [75, 77, 80, 86, 114, 130, 131, 153, 231, 247, 296, 312, 329]). Сети Хопфилда являются основным объектом исследования в модельном направлении нейроинформатики.
Формальная постановка задачи
Пусть задан набор из m эталонов – n-мерных векторов  . Требуется построить сеть, которая при предъявлении на вход произвольного образа – вектора x – давала бы на выходе «наиболее похожий» эталон. . Требуется построить сеть, которая при предъявлении на вход произвольного образа – вектора x – давала бы на выходе «наиболее похожий» эталон.
Всюду далее образы и, в том числе, эталоны – n-мерные векторы с координатами 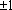 . Примером понятия эталона «наиболее похожего» на x может служить ближайший к x вектор . Примером понятия эталона «наиболее похожего» на x может служить ближайший к x вектор 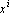 . Легко заметить, что это требование эквивалентно требованию максимальности скалярного произведения векторов x и . Легко заметить, что это требование эквивалентно требованию максимальности скалярного произведения векторов x и 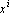 : : 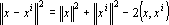 . Первые два слагаемых в правой части совпадают для любых образов x и . Первые два слагаемых в правой части совпадают для любых образов x и 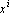 , так как длины всех векторов-образов равны , так как длины всех векторов-образов равны  . Таким образом, задача поиска ближайшего образа сводится к поиску образа, скалярное произведение с которым максимально. Этот простой факт приводит к тому, что сравнивать придется линейные функции от образов, тогда как расстояние является квадратичной функцией. . Таким образом, задача поиска ближайшего образа сводится к поиску образа, скалярное произведение с которым максимально. Этот простой факт приводит к тому, что сравнивать придется линейные функции от образов, тогда как расстояние является квадратичной функцией.
Сети Хопфилда
Наиболее известной сетью ассоциативной памяти является сеть Хопфилда [312]. В основе сети Хопфилда лежит следующая идея – запишем систему дифференциальных уравнений для градиентной минимизации «энергии» H (функции Ляпунова). Точки равновесия такой системы находятся в точках минимума энергии. Функцию энергии будем строить из следующих соображений:
- Каждый эталон должен быть точкой минимума.
- В точке минимума все координаты образа должны иметь значения
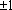 . .
Функция
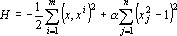
не удовлетворяет этим требованиям строго, но можно предполагать, что первое слагаемое обеспечит притяжение к эталонам (для вектора x фиксированной длины максимум квадрата скалярного произведения 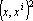 достигается при достигается при  ), а второе слагаемое ), а второе слагаемое 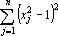 – приблизит к единице абсолютные величины всех координат точки минимума). Величина a характеризует соотношение между этими двумя требованиями и может меняться со временем. – приблизит к единице абсолютные величины всех координат точки минимума). Величина a характеризует соотношение между этими двумя требованиями и может меняться со временем.
Используя выражение для энергии, можно записать систему уравнений, описывающих функционирование сети Хопфилда [312]:
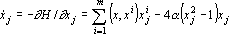 . . |
(1) |
Сеть Хопфилда в виде (1) является сетью с непрерывным временем. Это, быть может, и удобно для некоторых вариантов аналоговой реализации, но для цифровых компьютеров лучше воспользоваться сетями, функционирующими в дискретном времени – шаг за шагом.
Построим сеть Хопфилда [312] с дискретным временем. Сеть должна осуществлять преобразование входного вектора x так, чтобы выходной вектор 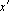 был ближе к тому эталону, который является правильным ответом. Преобразование сети будем искать в следующем виде: был ближе к тому эталону, который является правильным ответом. Преобразование сети будем искать в следующем виде:
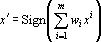 , , |
(2) |
где 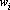 – вес i-го эталона, характеризующий его близость к вектору x, Sign - нелинейный оператор, переводящий вектор с координатами yi в вектор с координатами sign(yi). – вес i-го эталона, характеризующий его близость к вектору x, Sign - нелинейный оператор, переводящий вектор с координатами yi в вектор с координатами sign(yi).
Функционирование сети
Сеть работает следующим образом:
- На вход сети подается образ x, а на выходе снимается образ
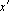 . .
- Если
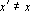 , то полагаем , то полагаем 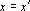 и возвращаемся к шагу 1. и возвращаемся к шагу 1.
- Полученный вектор
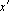 является ответом. является ответом.
Таким образом, ответ всегда является неподвижной точкой преобразования сети (2) и именно это условие (неизменность при обработке образа сетью) и является условием остановки.
Пусть  – номер эталона, ближайшего к образу x. Тогда, если выбрать веса пропорционально близости эталонов к исходному образу x, то следует ожидать, что образ – номер эталона, ближайшего к образу x. Тогда, если выбрать веса пропорционально близости эталонов к исходному образу x, то следует ожидать, что образ 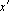 будет ближе к эталону будет ближе к эталону 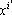 , чем x, а после нескольких итераций он станет совпадать с эталоном , чем x, а после нескольких итераций он станет совпадать с эталоном 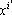 . .
Наиболее простой сетью вида (2) является дискретный вариант сети Хопфилда [312] с весами равными скалярному произведению эталонов на предъявляемый образ:
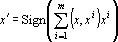 . . |
(3) |

Рис. 1. а, б, в – эталоны,
г – ответ сети на предъявление любого эталона |
О сетях Хопфилда (3) известно [53, 231, 247, 312], что они способны запомнить и точно воспроизвести «порядка 0.14n слабо коррелированных образов». В этом высказывании содержится два ограничения:
- число эталонов не превосходит 0.14n.
- эталоны слабо коррелированны.
Наиболее существенным является второе ограничение, поскольку образы, которые сеть должна обрабатывать, часто очень похожи. Примером могут служить буквы латинского алфавита. При обучении сети Хопфилда (3) распознаванию трех первых букв (см. рис. 1 а, б, в), при предъявлении на вход сети любого их эталонов в качестве ответа получается образ, приведенный на рис. 1 г (все образы брались в рамке 10 на 10 точек).
В связи с такими примерами первый вопрос о качестве работы сети ассоциативной памяти звучит тривиально: будет ли сеть правильно обрабатывать сами эталонные образы (т.е. не искажать их)?
Мерой коррелированности образов будем называть следующую величину:
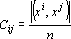
Зависимость работы сети Хопфилда от степени коррелированности образов можно легко продемонстрировать на следующем примере. Пусть даны три эталона 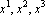 таких, что таких, что
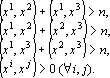 |
(4) |
Для любой координаты существует одна из четырех возможностей:
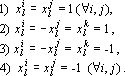
В первом случае при предъявлении сети q-го эталона в силу формулы (3) получаем 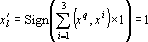 , так как все скалярные произведения положительны по условию (4). Аналогично получаем в четвертом случае , так как все скалярные произведения положительны по условию (4). Аналогично получаем в четвертом случае 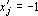 . .
Во втором случае рассмотрим отдельно три варианта
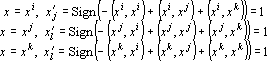
так как скалярный квадрат любого образа равен n, а сумма двух любых скалярных произведений эталонов больше n, по условию (4). Таким образом, независимо от предъявленного эталона получаем 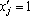 . Аналогично в третьем случае получаем . Аналогично в третьем случае получаем 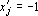 . .
Окончательный вывод таков: если эталоны удовлетворяют условиям (4), то при предъявлении любого эталона на выходе всегда будет один образ. Этот образ может быть эталоном или «химерой», составленной, чаще всего, из узнаваемых фрагментов различных эталонов (примером «химеры» может служить образ, приведенный на рис. 1г). Рассмотренный ранее пример с буквами детально иллюстрирует такую ситуацию.
Приведенные выше соображения позволяют сформулировать требование, детализирующие понятие «слабо коррелированных образов». Для правильного распознавания всех эталонов достаточно (но не необходимо) потребовать, чтобы выполнялось следующее неравенство 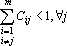 . Более простое и наглядное, хотя и более сильное условие можно записать в виде . Более простое и наглядное, хотя и более сильное условие можно записать в виде 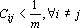 . Из этих условий видно, что, чем больше задано эталонов, тем более жесткие требования предъявляются к степени их коррелированности, тем ближе они должны быть к ортогональным. . Из этих условий видно, что, чем больше задано эталонов, тем более жесткие требования предъявляются к степени их коррелированности, тем ближе они должны быть к ортогональным.
Рассмотрим преобразование (3) как суперпозицию двух преобразований:
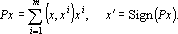 |
(5) |
Обозначим через 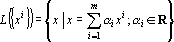 – линейное пространство, натянутое на множество эталонов. Тогда первое преобразование в (5) переводит векторы из – линейное пространство, натянутое на множество эталонов. Тогда первое преобразование в (5) переводит векторы из 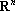 в в 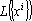 . Второе преобразование в (5) переводит результат первого преобразования Px в одну из вершин гиперкуба образов. Легко показать, что второе преобразование в (5) переводит точку Px в ближайшую вершину гиперкуба. Действительно, пусть a и b две различные вершины гиперкуба такие, что a – ближайшая к Px, а . Второе преобразование в (5) переводит результат первого преобразования Px в одну из вершин гиперкуба образов. Легко показать, что второе преобразование в (5) переводит точку Px в ближайшую вершину гиперкуба. Действительно, пусть a и b две различные вершины гиперкуба такие, что a – ближайшая к Px, а 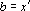 . Из того, что a и b различны следует, что существует множество индексов, в которых координаты векторов a и b различны. Обозначим это множество через . Из того, что a и b различны следует, что существует множество индексов, в которых координаты векторов a и b различны. Обозначим это множество через 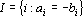 . Из второго преобразования в (5) и того, что . Из второго преобразования в (5) и того, что 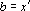 , следует, что знаки координат вектора Px всегда совпадают со знаками соответствующих координат вектора b. Учитывая различие знаков i-х координат векторов a и Px при , следует, что знаки координат вектора Px всегда совпадают со знаками соответствующих координат вектора b. Учитывая различие знаков i-х координат векторов a и Px при 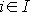 можно записать можно записать 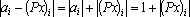 . Совпадение знаков i-х координат векторов b и Px при . Совпадение знаков i-х координат векторов b и Px при 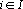 позволяет записать следующее неравенство позволяет записать следующее неравенство 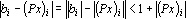 . Сравним расстояния от вершин a и b до точки Px . Сравним расстояния от вершин a и b до точки Px
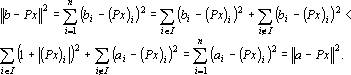
Полученное неравенство  противоречит тому, что a – ближайшая к Px. Таким образом, доказано, что второе преобразование в (5) переводит точку Px в ближайшую вершину гиперкуба образов. противоречит тому, что a – ближайшая к Px. Таким образом, доказано, что второе преобразование в (5) переводит точку Px в ближайшую вершину гиперкуба образов.
Ортогональные сети
Для обеспечения правильного воспроизведения эталонов вне зависимости от степени их коррелированности достаточно потребовать, чтобы первое преобразование в (5) было таким, что 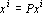 [67]. Очевидно, что если проектор является ортогональным, то это требование выполняется, поскольку [67]. Очевидно, что если проектор является ортогональным, то это требование выполняется, поскольку 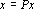 при при 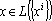 , а , а 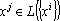 по определению множества по определению множества 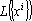 . .
Для обеспечения ортогональности проектора воспользуемся дуальным множеством векторов. Множество векторов 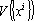 называется дуальным к множеству векторов называется дуальным к множеству векторов 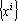 , если все векторы этого множества , если все векторы этого множества 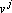 удовлетворяют следующим требованиям: удовлетворяют следующим требованиям:
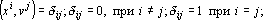
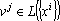 . .
Преобразование 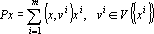 является ортогональным проектором на линейное пространство является ортогональным проектором на линейное пространство 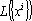 . .
Ортогональная сеть ассоциативной памяти преобразует образы по формуле
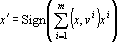 . . |
(6) |
Дуальное множество векторов существует тогда и только тогда, когда множество векторов 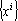 линейно независимо. Если множество эталонов линейно независимо. Если множество эталонов 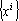 линейно зависимо, то исключим из него линейно зависимые образы и будем рассматривать полученное усеченное множество эталонов как основу для построения дуального множества и преобразования (6). Образы, исключенные из исходного множества эталонов, будут по-прежнему сохраняться сетью в исходном виде (преобразовываться в самих себя). Действительно, пусть эталон x является линейно зависимым от остальных m эталонов. Тогда его можно представить в виде линейно зависимо, то исключим из него линейно зависимые образы и будем рассматривать полученное усеченное множество эталонов как основу для построения дуального множества и преобразования (6). Образы, исключенные из исходного множества эталонов, будут по-прежнему сохраняться сетью в исходном виде (преобразовываться в самих себя). Действительно, пусть эталон x является линейно зависимым от остальных m эталонов. Тогда его можно представить в виде 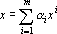 . Подставив полученное выражение в преобразование (6) и учитывая свойства дуального множества получим: . Подставив полученное выражение в преобразование (6) и учитывая свойства дуального множества получим:
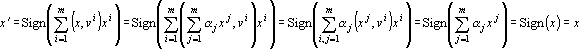 |
(7) |
Рассмотрим свойства сети (6) [67]. Во-первых, количество запоминаемых и точно воспроизводимых эталонов не зависит от степени их коррелированности. Во-вторых, формально сеть способна работать без искажений при любом возможном числе эталонов (всего их может быть до 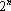 ). Однако, если число линейно независимых эталонов (т.е. ранг множества эталонов) равно n, сеть становится прозрачной – какой бы образ не предъявили на ее вход, на выходе окажется тот же образ. Действительно, как было показано в (7), все образы, линейно зависимые от эталонов, преобразуются проективной частью преобразования (6) сами в себя. Значит, если в множестве эталонов есть n линейно независимых, то любой образ можно представить в виде линейной комбинации эталонов (точнее n линейно независимых эталонов), а проективная часть преобразования (6) в силу формулы (7) переводит любую линейную комбинацию эталонов в саму себя. ). Однако, если число линейно независимых эталонов (т.е. ранг множества эталонов) равно n, сеть становится прозрачной – какой бы образ не предъявили на ее вход, на выходе окажется тот же образ. Действительно, как было показано в (7), все образы, линейно зависимые от эталонов, преобразуются проективной частью преобразования (6) сами в себя. Значит, если в множестве эталонов есть n линейно независимых, то любой образ можно представить в виде линейной комбинации эталонов (точнее n линейно независимых эталонов), а проективная часть преобразования (6) в силу формулы (7) переводит любую линейную комбинацию эталонов в саму себя.
Если число линейно независимых эталонов меньше n, то сеть преобразует поступающий образ, отфильтровывая помехи, ортогональные всем эталонам.
Отметим, что результаты работы сетей (3) и (6) эквивалентны, если все эталоны попарно ортогональны.
Остановимся несколько подробнее на алгоритме вычисления дуального множества векторов. Обозначим через 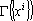 матрицу Грама множества векторов матрицу Грама множества векторов 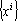 . Элементы матрицы Грама имеют вид . Элементы матрицы Грама имеют вид 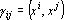 (ij-ый элемент матрицы Грама равен скалярному произведению i-го эталона на j-ый). Известно, что векторы дуального множества можно записать в следующем виде: (ij-ый элемент матрицы Грама равен скалярному произведению i-го эталона на j-ый). Известно, что векторы дуального множества можно записать в следующем виде:
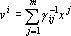 , , |
(8) |
где 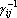 – элемент матрицы – элемент матрицы 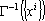 . Поскольку определитель матрицы Грама равен нулю, если множество векторов линейно зависимо, то матрица, обратная к матрице Грама, а следовательно и дуальное множество векторов существует только тогда, когда множество эталонов линейно независимо. . Поскольку определитель матрицы Грама равен нулю, если множество векторов линейно зависимо, то матрица, обратная к матрице Грама, а следовательно и дуальное множество векторов существует только тогда, когда множество эталонов линейно независимо.
Для работ сети (6) необходимо хранить эталоны и матрицу 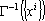 . .
Рассмотрим процедуру добавления нового эталона к сети (6). Эта операция часто называется дообучением сети. Важным критерием оценки алгоритма формирования сети является соотношение вычислительных затрат на обучение и дообучение. Затраты на дообучение не должны зависеть от числа освоенных ранее эталонов.
Для сетей Хопфилда это, очевидно, выполняется – добавление еще одного эталона сводится к прибавлению к функции H одного слагаемого 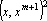 , а модификация связей в сети – состоит в прибавлении к весу ij-й связи числа , а модификация связей в сети – состоит в прибавлении к весу ij-й связи числа 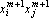 – всего – всего 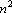 операций. операций.
Для рассматриваемых сетей с ортогональным проектированием также возможно простое дообучение. На первый взгляд, это может показаться странным – если добавляемый эталон линейно независим от старых эталонов, то, вообще говоря, необходимо пересчитать матрицу Грама и обратить ее. Однако симметричность матрицы Грама позволяет не производить заново процедуру обращения всей матрицы. Действительно, обозначим через 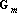 – матрицу Грама для множества из m векторов; через – матрицу Грама для множества из m векторов; через 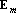 – единичную матрицу размерности – единичную матрицу размерности 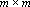 . При обращении матриц методом Гаусса используется следующая процедура: . При обращении матриц методом Гаусса используется следующая процедура:
- Запишем матрицу размерности
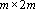 следующего вида: следующего вида: 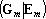 . .
- Используя операции сложения строк и умножения строки на ненулевое число преобразуем левую квадратную подматрицу к единичной. В результате получим
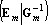 . .
Пусть известна 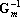 – обратная к матрице Грама для множества из m векторов – обратная к матрице Грама для множества из m векторов 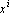 . Добавим к этому множеству вектор . Добавим к этому множеству вектор 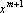 . Тогда матрица для обращения матрицы . Тогда матрица для обращения матрицы 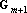 методом Гауса будет иметь вид: методом Гауса будет иметь вид:
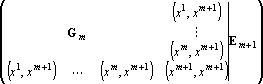 . .
После приведения к единичной матрице главного минора ранга m получится следующая матрица:
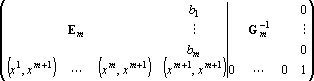 , ,
где 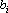 – неизвестные величины, полученные в ходе приведения главного минора к единичной матрице. Для завершения обращения матрицы – неизвестные величины, полученные в ходе приведения главного минора к единичной матрице. Для завершения обращения матрицы 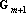 необходимо привести к нулевому виду первые m элементов последней строки и (m+1)-о столбца. Для обращения в ноль i-о элемента последней строки необходимо умножить i-ю строку на необходимо привести к нулевому виду первые m элементов последней строки и (m+1)-о столбца. Для обращения в ноль i-о элемента последней строки необходимо умножить i-ю строку на 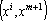 и вычесть из последней строки. После проведения этого преобразования получим и вычесть из последней строки. После проведения этого преобразования получим
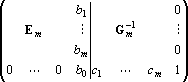 , ,
где 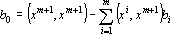 , , 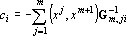 . . 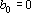 только если новый эталон является линейной комбинацией первых m эталонов. Следовательно только если новый эталон является линейной комбинацией первых m эталонов. Следовательно 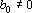 . Для завершения обращения необходимо разделить последнюю строку на . Для завершения обращения необходимо разделить последнюю строку на 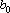 и затем вычесть из всех предыдущих строк последнюю, умноженную на соответствующее номеру строки и затем вычесть из всех предыдущих строк последнюю, умноженную на соответствующее номеру строки 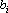 . В результате получим следующую матрицу . В результате получим следующую матрицу
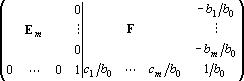 , ,
где 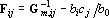 . Поскольку матрица, обратная к симметричной, всегда симметрична получаем . Поскольку матрица, обратная к симметричной, всегда симметрична получаем 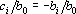 при всех i. Так как при всех i. Так как 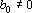 следовательно следовательно 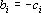 . .
Обозначим через d вектор 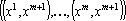 , через b – вектор , через b – вектор 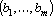 . Используя эти обозначения можно записать . Используя эти обозначения можно записать 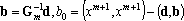 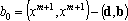 . Матрица . Матрица 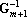 записывается в виде записывается в виде
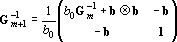 . .
Таким образом, при добавлении нового эталона требуется произвести следующие операции:
- Вычислить вектор d (m скалярных произведений – mn операций,
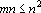 ). ).
- Вычислить вектор b (умножение вектора на матрицу –
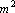 операций). операций).
- Вычислить
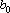 (два скалярных произведения – m+n операций). (два скалярных произведения – m+n операций).
- Умножить матрицу на число и добавить тензорное произведение вектора b на себя (
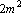 операций). операций).
- Записать
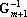 . .
Таким образом эта процедура требует 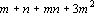 операций. Тогда как стандартная схема полного пересчета потребует: операций. Тогда как стандартная схема полного пересчета потребует:
- Вычислить всю матрицу Грама (
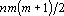 операций). операций).
- Методом Гаусса привести левую квадратную матрицу к единичному виду (
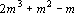 операций). операций).
- Записать
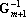 . .
Всего 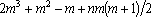 операций, что в m раз больше. операций, что в m раз больше.
Используя ортогональную сеть (6), удалось добиться независимости способности сети к запоминанию и точному воспроизведению эталонов от степени коррелированности эталонов. Так, например, ортогональная сеть смогла правильно воспроизвести все буквы латинского алфавита в написании, приведенном на рис. 1.
Основным ограничением сети (6) является малое число эталонов – число линейно независимых эталонов должно быть меньше размерности системы n.
Тензорные сети
Для увеличения числа линейно независимых эталонов, не приводящих к прозрачности сети, используется прием перехода к тензорным или многочастичным сетям [75, 86, 93, 293].
В тензорных сетях используются тензорные степени векторов. k-ой тензорной степенью вектора x будем называть тензор 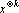 , полученный как тензорное произведение k векторов x. Поскольку в данной работе тензоры используются только как элементы векторного пространства, далее будем использовать термин вектор вместо тензор. Вектор , полученный как тензорное произведение k векторов x. Поскольку в данной работе тензоры используются только как элементы векторного пространства, далее будем использовать термин вектор вместо тензор. Вектор 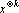 является является 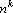 -мерным вектором. Однако пространство -мерным вектором. Однако пространство 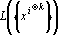 имеет размерность, не превышающую величину имеет размерность, не превышающую величину 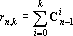 , где , где 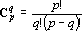 – число сочетаний из p по q. Обозначим через – число сочетаний из p по q. Обозначим через 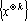 множество k-х тензорных степеней всех возможных образов. множество k-х тензорных степеней всех возможных образов.
Теорема. При k<n в множестве 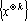 линейно независимыми являются линейно независимыми являются 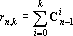 векторов. Доказательство теоремы приведено в последнем разделе данной главы. векторов. Доказательство теоремы приведено в последнем разделе данной главы.
| |
2 |
|
| |
3 |
4 |
|
| |
4 |
7 |
8 |
|
| |
5 |
11 |
15 |
16 |
|
| |
6 |
16 |
26 |
31 |
32 |
|
| |
7 |
22 |
42 |
57 |
63 |
64 |
|
| |
8 |
29 |
64 |
99 |
120 |
127 |
128 |
|
| |
9 |
37 |
93 |
163 |
219 |
247 |
255 |
256 |
|
| |
10 |
46 |
130 |
256 |
382 |
466 |
502 |
511 |
512 |
|
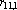 |
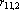 |
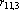 |
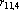 |
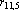 |
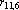 |
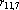 |
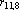 |
 |
 |
| Рис. 2. “Тензорный” треугольник Паскаля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Небольшая модернизация треугольника Паскаля, позволяет легко вычислять эту величину. На рис. 2 приведен «тензорный» треугольник Паскаля. При его построении использованы следующие правила:
1. Первая строка содержит двойку, поскольку при n=2 в множестве X всего два неколлинеарных вектора.
2. При переходе к новой строке, первый элемент получается добавлением единицы к первому элементу предыдущей строки, второй – как сумма первого и второго элементов предыдущей строки, третий – как сумма второго и третьего элементов и т.д. Последний элемент получается удвоением последнего элемента предыдущей строки.
Таблица 1.
| n |
k |
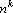 |
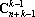 |
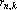 |
| 5 |
2 |
25 |
15 |
11 |
| |
3 |
125 |
35 |
15 |
| 10 |
3 |
1 000 |
220 |
130 |
| |
6 |
1 000 000 |
5005 |
466 |
| |
8 |
100 000 000 |
24310 |
511 | |
В табл. 1 приведено сравнение трех оценок информационной емкости тензорных сетей для некоторых значений n и k. Первая оценка – 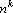 – заведомо завышена, вторая – – заведомо завышена, вторая – 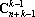 – дается формулой Эйлера для размерности пространства симметричных тензоров и третья – точное значение – дается формулой Эйлера для размерности пространства симметричных тензоров и третья – точное значение 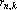
Как легко видеть из таблицы, уточнение при переходе к оценке 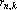 является весьма существенным. С другой стороны, предельная информационная емкость тензорной сети (число правильно воспроизводимых образов) может существенно превышать число нейронов, например, для 10 нейронов тензорная сеть валентности 8 имеет предельную информационную емкость 511. является весьма существенным. С другой стороны, предельная информационная емкость тензорной сети (число правильно воспроизводимых образов) может существенно превышать число нейронов, например, для 10 нейронов тензорная сеть валентности 8 имеет предельную информационную емкость 511.
Легко показать, что если множество векторов 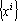 не содержит противоположно направленных, то размерность пространства не содержит противоположно направленных, то размерность пространства 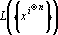 равна числу векторов в множестве равна числу векторов в множестве 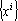 . .
Сеть (2) для случая тензорных сетей имеет вид
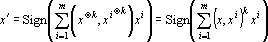 , , |
(9) |
а ортогональная тензорная сеть
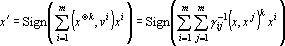 , , |
(10) |
где 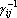 – элемент матрицы – элемент матрицы 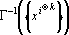 . .
Рассмотрим, как изменяется степень коррелированности эталонов при переходе к тензорным сетям (9)
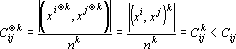 . .
Таким образом, при использовании сетей (9) сильно снижается ограничение на степень коррелированности эталонов. Для эталонов, приведенных на рис.1, данные о степени коррелированности эталонов для нескольких тензорных степеней приведены в табл. 2.
Таблица 2
Степени коррелированности эталонов, приведенных на рис. 1, для различных тензорных степеней.
| Тензорная степень |
Степень коррелированности |
Условия |
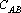 |
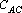 |
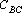 |
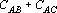 |
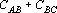 |
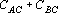 |
| 1 |
0.74 |
0.72 |
0.86 |
1.46 |
1.60 |
1.58 |
| 2 |
0.55 |
0.52 |
0.74 |
1.07 |
1.29 |
1.26 |
| 3 |
0.41 |
0.37 |
0.64 |
0.78 |
1.05 |
1.01 |
| 4 |
0.30 |
0.26 |
0.55 |
0.56 |
0.85 |
0.81 |
| 5 |
0.22 |
0.19 |
0.47 |
0.41 |
0.69 |
0.66 |
| 6 |
0.16 |
0.14 |
0.40 |
0.30 |
0.56 |
0.54 |
| 7 |
0.12 |
0.10 |
0.35 |
0.22 |
0.47 |
0.45 |
| 8 |
0.09 |
0.07 |
0.30 |
0.16 |
0.39 |
0.37 |
Анализ данных, приведенных в табл. 2, показывает, что при тензорных степенях 1, 2 и 3 степень коррелированности эталонов не удовлетворяет первому из достаточных условий (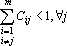 ), а при степенях меньше 8 – второму ( ), а при степенях меньше 8 – второму (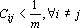 ). ).
Таким образом, чем выше тензорная степень сети (9), тем слабее становится ограничение на степень коррелированности эталонов. Сеть (10) не чувствительна к степени коррелированности эталонов.
Сети для инвариантной обработки изображений
Для того, чтобы при обработке переводить визуальные образов, отличающиеся только положением в рамке изображения, в один эталон, применяется следующий прием [91]. Преобразуем исходное изображение в некоторый вектор величин, не изменяющихся при сдвиге (вектор инвариантов). Простейший набор инвариантов дают автокорреляторы – скалярные произведения образа на сдвинутый образ, рассматриваемые как функции вектора сдвига.
В качестве примера рассмотрим вычисление сдвигового автокоррелятора для черно-белых изображений. Пусть дан двумерный образ S размером 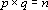 . Обозначим точки образа как . Обозначим точки образа как 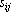 . Элементами автокоррелятора . Элементами автокоррелятора 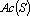 будут величины будут величины 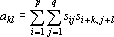 , где , где 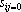 при выполнении любого из неравенств при выполнении любого из неравенств 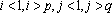 . Легко проверить, что автокорреляторы любых двух образов, отличающихся только расположением в рамке, совпадают. Отметим, что . Легко проверить, что автокорреляторы любых двух образов, отличающихся только расположением в рамке, совпадают. Отметим, что 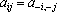 при всех i,j, и при всех i,j, и 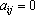 при выполнении любого из неравенств при выполнении любого из неравенств 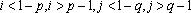 . Таким образом, можно считать, что размер автокоррелятора равен . Таким образом, можно считать, что размер автокоррелятора равен 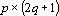 . .
Автокорреляторная сеть имеет вид
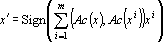 . . |
(11) |
Сеть (11) позволяет обрабатывать различные визуальные образы, отличающиеся только положением в рамке, как один образ.
Конструирование сетей под задачу
Подводя итоги, можно сказать, что все сети ассоциативной памяти типа (2) можно получить, комбинируя следующие преобразования:
- Произвольное преобразование. Например, переход к автокорреляторам, позволяющий объединять в один выходной образ все образы, отличающиеся только положением в рамке.
- Тензорное преобразование, позволяющее сильно увеличить способность сети запоминать и точно воспроизводить эталоны.
- Переход к ортогональному проектору, снимающий зависимость надежности работы сети от степени коррелированности образов.
Наиболее сложная сеть будет иметь вид:
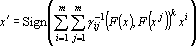 , , |
(12) |
где 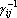 – элементы матрицы, обратной матрице Грама системы векторов – элементы матрицы, обратной матрице Грама системы векторов 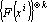 , , 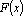 – произвольное преобразование. – произвольное преобразование.
Возможно применение и других методов предобработки. Некоторые из них рассмотрены в работах [68, 91, 278]
Численный эксперимент
Работа ортогональных тензорных сетей при наличии помех сравнивалась с возможностями линейных кодов, исправляющих ошибки. Линейным кодом, исправляющим k ошибок, называется линейное подпространство в n-мерном пространстве над GF2, все вектора которого удалены друг от друга не менее чем на 2k+1. Линейный код называется совершенным, если для любого вектора n-мерного пространства существует кодовый вектор, удаленный от данного не более, чем на k. Тензорной сети в качестве эталонов подавались все кодовые векторы избранного для сравнения кода. Численные эксперименты с совершенными кодами показали, что тензорная сеть минимально необходимой валентности правильно декодирует все векторы. Для несовершенных кодов картина оказалась хуже – среди устойчивых образов тензорной сети появились «химеры» – векторы, не принадлежащие множеству эталонов.
Таблица 3
Результаты численного эксперимента.
МР – минимальное расстояние между эталонами, ЧЭ – число эталонов
| № |
Раз-
Мер- ность |
Число векто-
ров |
МР |
ЧЭ |
Валент-ность |
Число химер |
Число
ответов |
После обработки сетью расстояние до правильного ответа стало |
| верн. |
неверн. |
меньше |
то же |
больше |
| 1 |
10 |
1024 |
3 |
64 |
3¸5 |
896 |
128 |
896 |
0 |
856 |
0 |
| 2 |
|
|
|
|
7¸21 |
384 |
640 |
384 |
0 |
348 |
0 |
| 3 |
10 |
1024 |
5 |
8 |
3 |
260 |
464 |
560 |
240 |
260 |
60 |
| 4 |
|
|
|
|
5¸15 |
230 |
494 |
530 |
240 |
230 |
60 |
| 5 |
|
|
|
|
17¸21 |
140 |
532 |
492 |
240 |
182 |
70 |
| 6 |
15 |
32768 |
7 |
32 |
3 |
15456 |
17312 |
15456 |
0 |
15465 |
0 |
| 7 |
|
|
|
|
5¸21 |
14336 |
18432 |
14336 |
0 |
14336 |
0 |
В случае n=10, k=1 (см. табл. 3 и 4, строка 1) при валентностях 3 и 5 тензорная сеть работала как единичный оператор – все входные вектора передавались на выход сети без изменений. Однако уже при валентности 7 число химер резко сократилось и сеть правильно декодировала более 60% сигналов. При этом были правильно декодированы все векторы, удаленные от ближайшего эталона на расстояние 2, а часть векторов, удаленных от ближайшего эталона на расстояние 1, остались химерами. В случае n=10, k=2 (см. табл. 3 и 4, строки 3, 4, 5) наблюдалось уменьшение числа химер с ростом валентности, однако часть химер, удаленных от ближайшего эталона на расстояние 2 сохранялась. Сеть правильно декодировала более 50% сигналов. Таким образом при малых размерностях и кодах, далеких от совершенных, тензорная сеть работает довольно плохо. Однако, уже при n=15, k=3 и валентности, большей 3 (см. табл. 3 и 4, строки 6, 7), сеть правильно декодировала все сигналы с тремя ошибками. В большинстве экспериментов число эталонов было больше числа нейронов.
Таблица 4.
Результаты численного эксперимента
№ |
Число химер, удаленных
от ближайшего эталона на: |
Число неверно распознанных векторов, удаленных от ближайшего эталона на: |
| |
1 |
2 |
3 |
4 |
5 |
1 |
2 |
3 |
4 |
5 |
| 1 |
640 |
256 |
0 |
0 |
0 |
896 |
0 |
0 |
0 |
0 |
| 2 |
384 |
0 |
0 |
0 |
0 |
384 |
0 |
0 |
0 |
0 |
| 3 |
0 |
210 |
50 |
0 |
0 |
0 |
210 |
290 |
60 |
0 |
| 4 |
0 |
180 |
50 |
0 |
0 |
0 |
180 |
290 |
60 |
0 |
| 5 |
0 |
88 |
50 |
2 |
0 |
0 |
156 |
290 |
60 |
0 |
| 6 |
0 |
0 |
1120 |
13440 |
896 |
0 |
0 |
1120 |
13440 |
896 |
| 7 |
0 |
0 |
0 |
13440 |
896 |
0 |
0 |
0 |
13440 |
896 |
Подводя итог можно сказать, что качество работы сети возрастает с ростом размерности пространства и валентности и по эффективности устранения ошибок сеть приближается к коду, гарантированно исправляющему ошибки.
Доказательство теоремы
В данном разделе приведено доказательство теоремы о числе линейно независимых образов в пространстве k-х тензорных степеней эталонов.
При построении тензорных сетей используются тензоры валентности k следующего вида:
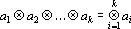 , , |
(13) |
где  – n-мерные вектора над полем действительных чисел. – n-мерные вектора над полем действительных чисел.
Если все вектора 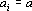 , то будем говорить о k-й тензорной степени вектора a, и использовать обозначение , то будем говорить о k-й тензорной степени вектора a, и использовать обозначение 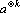 . Для дальнейшего важны следующие элементарные свойства тензоров вида (13). . Для дальнейшего важны следующие элементарные свойства тензоров вида (13).
1. Пусть 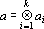 и и 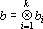 , тогда скалярное произведение этих векторов может быть вычислено по формуле , тогда скалярное произведение этих векторов может быть вычислено по формуле
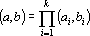 . . |
(14) |
Доказательство этого свойства следует непосредственно из свойств тензоров общего вида.
2. Если в условиях свойства 1 вектора являются тензорными степенями, то скалярное произведение имеет вид:
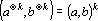 . . |
(15) |
Доказательство непосредственно вытекает из свойства 1.
3. Если вектора a и b ортогональны, то есть 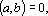 то и их тензорные степени любой положительной валентности ортогональны. то и их тензорные степени любой положительной валентности ортогональны.
Доказательство вытекает из свойства 2.
4. Если вектора a и b коллинеарны, то есть 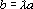 , то , то 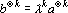 . .
Следствие. Если множество векторов 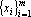 содержит хотя бы одну пару противоположно направленных векторов, то система векторов содержит хотя бы одну пару противоположно направленных векторов, то система векторов 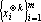 будет линейно зависимой при любой валентности k. будет линейно зависимой при любой валентности k.
5. Применение к множеству векторов 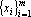 невырожденного линейного преобразования B в пространстве невырожденного линейного преобразования B в пространстве 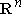 эквивалентно применению к множеству векторов эквивалентно применению к множеству векторов 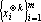 линейного невырожденного преобразования, индуцированного преобразованием B, в пространстве линейного невырожденного преобразования, индуцированного преобразованием B, в пространстве 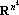 . .
Сюръективным мультииндексом 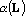 над конечным множеством L назовем k-мерный вектор, обладающий следующими свойствами: над конечным множеством L назовем k-мерный вектор, обладающий следующими свойствами:
1. для любого 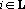 существует существует 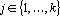 такое, что такое, что 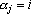 ; ;
2. для любого 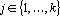 существует существует 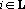 такое, что такое, что 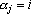 . .
Обозначим через 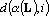 число компонент сюръективного мультииндекса число компонент сюръективного мультииндекса 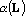 равных i, через равных i, через 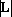 – число элементов множества L, а через – число элементов множества L, а через 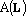 – множество всех сюръективных мультииндексов над множеством L. – множество всех сюръективных мультииндексов над множеством L.
Предложение 1. Если вектор a представлен в виде 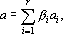 где где 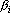 – произвольные действительные коэффициенты, то верно следующее равенство – произвольные действительные коэффициенты, то верно следующее равенство
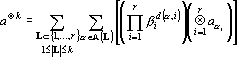 |
(16) |
Доказательство предложения получается возведением 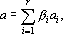 в тензорную степень k и раскрытием скобок с учетом линейности операции тензорного умножения. в тензорную степень k и раскрытием скобок с учетом линейности операции тензорного умножения.
В множестве 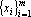 , выберем множество X следующим образом: возьмем все (n-1)-мерные вектора с координатами ±1, а в качестве n-й координаты во всех векторах возьмем единицу. , выберем множество X следующим образом: возьмем все (n-1)-мерные вектора с координатами ±1, а в качестве n-й координаты во всех векторах возьмем единицу.
Предложение 2. Множество X является максимальным множеством n-мерных векторов с координатами равными ±1 и не содержит пар противоположно направленных векторов.
Доказательство. Из равенства единице последней координаты всех векторов множества X следует отсутствие пар противоположно направленных векторов. Пусть x – вектор с координатами ±1, не входящий в множество X, следовательно последняя координата вектора x равна минус единице. Так как в множество X включались все (n-1)-мерные вектора с координатами ±1, то среди них найдется вектор, первые n-1 координата которого равны соответствующим координатам вектора x со знаком минус. Поскольку последние координаты также имеют противоположные знаки, то в множестве X нашелся вектор противоположно направленный по отношению к вектору x. Таким образом множество X максимально.
Таким образом в множестве X содержится ровно 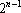 вектор. Каждый вектор вектор. Каждый вектор 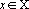 можно представить в виде можно представить в виде 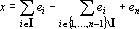 , где , где 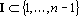 . Для нумерации векторов множества X будем использовать мультииндекс I. Обозначим через . Для нумерации векторов множества X будем использовать мультииндекс I. Обозначим через 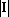 число элементов в мультииндексе I. Используя введенные обозначения можно разбить множество X на n непересекающихся подмножеств: число элементов в мультииндексе I. Используя введенные обозначения можно разбить множество X на n непересекающихся подмножеств: 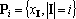 , , 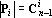 . .
Теорема. При k<n в множестве 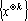 линейно независимыми являются линейно независимыми являются 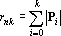 векторов. векторов.
Для доказательства этой теоремы потребуется следующая интуитивно очевидная, но не встреченная в литературе лемма.
Лемма. Пусть дана последовательность векторов
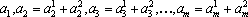
таких, что 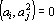 при всех при всех 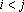 и и 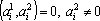 при всех i, тогда все вектора множества при всех i, тогда все вектора множества 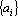 линейно независимы. линейно независимы.
Доказательство. Известно, что процедура ортогонализации Грама приводит к построению ортонормированного множества векторов, а все вектора линейно зависящие от предыдущих векторов последовательности обращаются в нулевые. Проведем процедуру ортогонализации для заданной последовательности векторов.
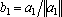
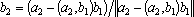 . Причем . Причем 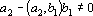 , так как , так как 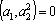 , , 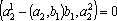 и и 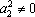 . .
...
j. 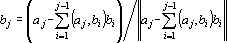 . Причем . Причем 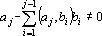 , так как , так как 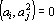 , при всех i<j, , при всех i<j,  и и 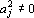 . .
...
Доказательство теоремы. Произведем линейное преобразование векторов множества X с матрицей 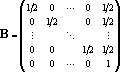 . Легко заметить, что при этом преобразовании все единичные координаты переходят в единичные, а координаты со значением -1 в нулевые. Таким образом . Легко заметить, что при этом преобразовании все единичные координаты переходят в единичные, а координаты со значением -1 в нулевые. Таким образом 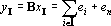 . По пятому свойству заключаем, что число линейно независимых векторов в множествах X и Y совпадает. Пусть . По пятому свойству заключаем, что число линейно независимых векторов в множествах X и Y совпадает. Пусть 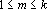 . Докажем, что . Докажем, что 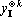 при при 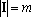 содержит компоненту, ортогональную всем содержит компоненту, ортогональную всем 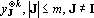 . Из предложения 1 имеем . Из предложения 1 имеем
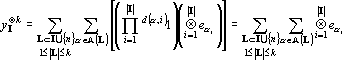 . . |
(17) |
Представим (17) в виде двух слагаемых:
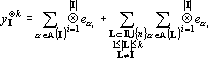 |
(18) |
Обозначим первую сумму в (18) через  . Докажем, что . Докажем, что  ортогонален ко всем ортогонален ко всем 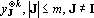 , и второй сумме в (18). Так как , и второй сумме в (18). Так как 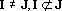 , существует , существует 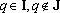 . Из свойств сюръективного мультииндекса следует, что все слагаемые, входящие в . Из свойств сюръективного мультииндекса следует, что все слагаемые, входящие в  содержат в качестве тензорного сомножителя содержат в качестве тензорного сомножителя 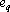 , не входящий ни в одно тензорное произведение, составляющие в сумме , не входящий ни в одно тензорное произведение, составляющие в сумме 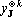 . Из свойства 2 получаем, что . Из свойства 2 получаем, что 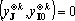 . Аналогично, из того, что в каждом слагаемом второй суммы . Аналогично, из того, что в каждом слагаемом второй суммы 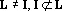 следует ортогональность следует ортогональность  каждому слагаемому второй суммы в (18) и, следовательно, всей сумме. каждому слагаемому второй суммы в (18) и, следовательно, всей сумме.
Таким образом 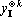 содержит компоненту содержит компоненту  ортогональную ко всем ортогональную ко всем 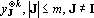 и и 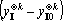 . Множество тензоров . Множество тензоров 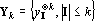 удовлетворяет условиям леммы, и следовательно все тензоры в удовлетворяет условиям леммы, и следовательно все тензоры в 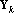 линейно независимы. Таким образом, число линейно независимых тензоров в множестве линейно независимы. Таким образом, число линейно независимых тензоров в множестве 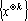 не меньше чем не меньше чем 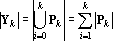 . .
Для того, чтобы показать, что число линейно независимых тензоров в множестве 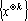 не превосходит этой величины достаточно показать, что добавление любого тензора из Y к не превосходит этой величины достаточно показать, что добавление любого тензора из Y к 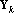 приводит к появлению линейной зависимости. Покажем, что любой приводит к появлению линейной зависимости. Покажем, что любой 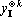 при при 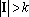 может быть представлен в виде линейной комбинации тензоров из может быть представлен в виде линейной комбинации тензоров из 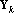 . Ранее было показано, что любой тензор . Ранее было показано, что любой тензор 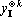 может быть представлен в виде (17). Разобьем (17) на три суммы: может быть представлен в виде (17). Разобьем (17) на три суммы:
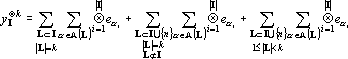 |
(19) |
Рассмотрим первое слагаемое в (19) отдельно.
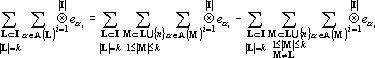 . .
Заменим в последнем равенстве внутреннюю сумму в первом слагаемом на тензоры из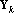 : :
 |
(20) |
Преобразуем второе слагаемое в (19).
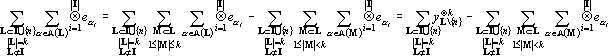 ( ( |
(21) |
Преобразуя аналогично (21) второе слагаемое в (20) и подставив результаты преобразований в (19) получим
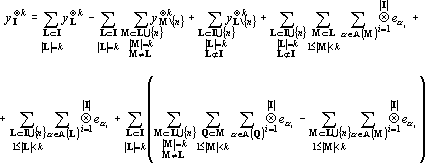 |
(22) |
В (22) все не замененные на тензоры из 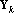 слагаемые содержат суммы по подмножествам множеств мощностью меньше k. Проводя аналогичную замену получим выражение, содержащее суммы по подмножествам множеств мощностью меньше k-1 и так далее. После завершения процедуры в выражении останутся только суммы содержащие вектора из слагаемые содержат суммы по подмножествам множеств мощностью меньше k. Проводя аналогичную замену получим выражение, содержащее суммы по подмножествам множеств мощностью меньше k-1 и так далее. После завершения процедуры в выражении останутся только суммы содержащие вектора из 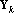 , то есть , то есть 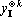 будет представлен в виде линейной комбинации векторов из будет представлен в виде линейной комбинации векторов из 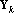 . Теорема доказана. . Теорема доказана.
Оглавление
| Введение
| П1
| П2
| П3
| Литература
Лекции:
1,
2-3,
4-6,
7.1,
7.2,
8,
9,
10,
11.1,
11.2-12,
13-14,
15-16
|