[ Часть 2 ]
Отсюда можно скачать полный текст обеих частей статьи в формате pdf (354 кб)
© 1996 А. А. Шалыто
Федеральный научно-производственный центр
ГУП "НПО "Аврора"",
Санкт-Петербургский государственный институт точной механики и оптики
(технический университет)
Статья опубликована журнале "Автоматика и телемеханика",
1996. N6, C.148-158; N7, С.144-169.
Имеется английская версия: Shalyto A.A.
Algorithmic graf schemes and transition graphs:
their
application in software realization
of logical control algorithms.
//Automation and Remote Control.
1996. N6, P.890-897; N7, P.1027-1045.
УДК 519.714
В работе выполнен
анализ недостатков, затрудняющих
понимание граф-схем алгоритмов и
программ, построенных на их
основе. Приведена классификация
граф-схем алгоритмов. Показано,
что основные трудности их
понимания возникают из-за
умолчаний и не использования в
них такого понятия как "состояние".
Введение этого понятия позволяет
переходить от граф-схем
алгоритмов к графам переходов.
Сформулированы требования к
графам переходов, выполнение
которых обеспечивает их "понятность".
1. Введение
В настоящее время
при программной реализации
алгоритмов логического управления
технологическими процессами
наряду с программируемыми
логическими контроллерами все чаще
используются компьютеры,
предназначенные для работы в
производственных условиях.
Однако вне
зависимости от типа управляющего
вычислительного устройства в силу
большой важности задач этого
класса (например, при управлении
ядерными реакторами) необходимо,
чтобы Заказчик, Разработчик,
Программист, Оператор и Контролер
однозначно и полностью понимали
друг друга.
Назовем язык
общения указанных сторон языком
спецификаций [1]. Несмотря на
наличие для задач логического
управления большого числа таких
языков [2-26] на практике, видимо, в
связи с традициями в области
вычислительной техники [5], наиболее
широкое использование в этом
качестве получили блок-схемы,
называемые также граф-схемами или
просто схемами [27, 28], что закреплено
соответствующими стандартами [29,
30].
Однако в этих
стандартах определяются лишь
правила изображения граф-схем и
отсутствуют требования (кроме
изобразительных) к их построению
для обеспечения возможности
легкого их понимания.
Необходимо
отметить, что и в литературе
недостаточно рассматривались
свойства граф-схемам алгоритмов,
упрощающие их применение в
качестве языка общения для
указанного класса задач. Так в [31,
32] были предложены
методы построения граф-схем,
структурная организация которых
улучшает их понимание. При этом
авторы этих работ считали, что если
граф-схемы построены только из
вложенных базовых управляющих
конструкций без использования
операторов go to, то это решает
проблему их легкого понимания и не
учитывали ряда других факторов,
затрудняющих чтение, и, в частности,
умолчания значений переменных.
Однако в
последнее время специалисты по
проектированию программ [33]
обратили внимание на то, что только
структурное проектирование
указанной проблемы не решает и
предложили объектно-ориентированный
подход к проектированию программ, в
рамках которого было введено
понятия "объекта" и его "состояния"
и рекомендовано использовать графы
переходов для описания динамики
реализуемых процессов. Однако,
кроме одного примера использования
графов переходов, эта работа не
содержит теоретического
обоснования требований к их
построению, обеспечивающих, в
частности, простоту понимания
программ.
В настоящей
работе разрабатываются требования
к построению легко понимаемых граф-схем
и графов переходов, а во второй ее
части предлагаются методы
построения понимаемых графов
переходов по граф-схемам
алгоритмов и понимаемых граф-схем
по графам переходов, а также методы
их программирования в базисе
языков различных уровней.
2. Граф-схемы. Основные
проблемы
Будем
рассматривать в настоящей работе
автоматные граф-схемы, в которых в
операторных вершинах формируются
или сохраняются только единичные и
нулевые значения переменных.
Автоматные граф-схемы разобьем на
два класса: граф-схемы алгоритмов и
граф-схемы программ.
При этом
будем различать граф-схемы
алгоритмов (ГСА) по следующим
основным признакам:
- наличию
внутренних обратных связей;
- используемым
типам переменных;
- наличию
дешифратора состояний;
- наличию
умолчаний и неоднозначно
задаваемых переменных;
- наличию
переменных, которые могут
неоднократно изменяться за
один проход граф-схемы;
- месту
выдачи значений выходных
переменных.
Используя
некоторые из этих признаков и не
претендуя на полноту классификации,
выделим пять подклассов граф-схем
алгоритмов:
- граф-схемы
алгоритмов с внутренними
обратными связями и выдачей
значений выходных переменных в
любой операторной вершине,
обозначаемые ГСА1;
- граф-схемы
алгоритмов без внутренних
обратных связей и дешифратора
состояний, в которых выдача
значений выходных переменных
выполняется в конце "тела"
граф-схемы, обозначаемые ГСА2;
- граф-схемы
алгоритмов без внутренних
обратных связей, учитывающие
особенности используемых
управляющих конструкций языка
программирования,
обозначаемые ГСА3;
- граф-схемы
алгоритмов без внутренних
обратных связей, но с
дешифратором состояний и
выдачей значений выходных
переменных в конце "тела"
граф-схемы, которые не содержат
выходных переменных,
неоднократно изменяющихся за
один проход граф-схемы,
обозначаемые ГСА4;
- граф-схемы
алгоритмов без внутренних
обратных связей, но с
дешифратором состояний и
выдачей значений выходных
переменных в конце "тела"
граф-схемы, содержащие
выходные переменные, которые
могут неоднократно изменяться
за один проход граф-схемы,
обозначаемые ГСА5.
При этом
отметим, что внешняя обратная связь
в управляющих алгоритмах и
программах существует всегда (режим
сканирования в программируемых
логических контроллерах). Отметим
также, что если в вычислительном
устройстве реализуется алгоритм
управления в виде одной компоненты
(задачи), то ГСА1, используя ГСА3,
могут при наличии соответствующих
управляющих конструкций изоморфно
отражаться в граф-схемы программ.
Если же
алгоритм управления реализуется в
вычислительном устройстве в виде
нескольких компонент, то для ГСА1
отсутствует возможность
изоморфного отражения в граф-схему
программы. Это объясняется тем, что
в задачах логического управления
при использовании ГСА1 при
определенных условиях на
длительное время может наступать
зацикливание по внутренним
обратным связям, что исключает
возможность перехода к реализации
других компонент алгоритма
управления до выхода из цикла.
Зацикливание может происходить,
например, до тех пор пока "не
нажата кнопка", "не сработал
сигнализатор", "не кончилась
выдержка времени" или "вал
не совершил несколько оборотов".
На рис.1 в
качестве примера приведена схема
связи управляющего автомата с
объектом управления, состоящим из
трех клапанов (Кл1, Кл2, Кл3) и
двигателя (Д). При этом управляющий
автомат декомпозирован на автомат (А)
и функциональные элементы задержки
(ФЭЗ).
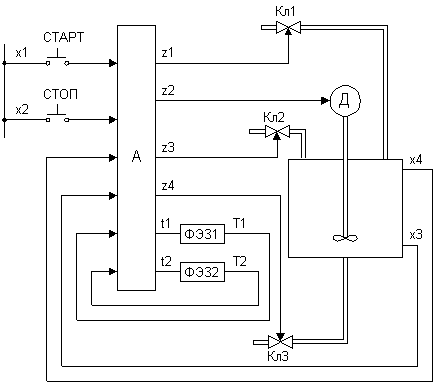
Рис. 1.
На рис.2 для
рассматриваемого примера
приведена ГСА1 с пятью внутренними
обратными связями [34].
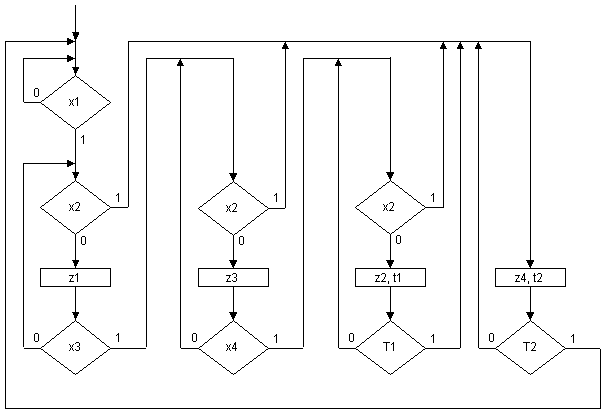
Рис. 2.
Эта граф-схема
реализует либо управляющий автомат
в целом (ФЭЗ1 и ФЭЗ2 вычисляются в
третьей и четвертой операторных
вершинах), либо только автомат (временные
переменные t1 и t2 рассматриваются
как обращения к процедуре,
реализующей функциональные
элементы задержки, а двоичные
переменные T1 и T2 сигнализируют о
срабатывании элементов задержки).
Эта граф-схема
содержательно неполна, так как в
ней не указано в каких операторных
вершинах сбрасываются выходные zi (i=1,...,4) и
временные tj (j=1, 2) переменные.
Поэтому эта граф-схема не может
использоваться в качестве
формальной спецификации задачи и
требует доопределения. Обращаясь к
принципам работы одновходовых
исполнительных механизмов,
используемых в рассматриваемом
объекте управления, можно
утверждать, что они не обладают
памятью и поэтому в ГСА1 (рис.2) по
умолчанию предполагается, что в тех
операторных вершинах, в которых
переменная не указана, ее значение
равно нулю.
Однако
предположение о том, что если в
операторных вершинах, в которых
некоторая выходная или временная
переменная отсутствует, то ее
значение равно нулю, справедливо
далеко не всегда, так как более
часто при использовании граф-схем
считают, что умалчиваемые
переменные сохраняют предыдущее
значение. Такие граф-схемы также
могут быть использованы для
вычислений, так как вычислительное
устройство помнит предыдущие
значения всех переменных,
сохраняющиеся во внешней по
отношению к граф-схемам памяти, но
они весьма трудно понимаются
человеком, которому сложно помнить
предысторию, особенно по
нескольким переменным
одновременно. При этом отметим, что
граф-схемы предназначены в
основном для отображения связей по
управлению и в существенно меньшей
степени - по данным [28, 35]. Таким образом,
граф-схемы с умалчиваемыми
значениями переменных
нецелесообразно применять в
качестве языка общения.
Поэтому
качественной можно считать только
такую спецификацию, в которой кроме
связей по управлению в
максимальной степени отражены
также и данные [35]. Отсутствие в
явном виде некоторых данных в граф-схемах
не позволяет использовать ее также
и в качестве теста для проверки
программы, реализующей эту граф-схему.
Более того, если программа строится
по граф-схеме эвристически, то даже
при отсутствии умолчаний с помощью
граф-схемы можно проверить лишь то,
что программа реализует граф-схему,
но невозможно установить, что
программа не делает ничего
дополнительно.
Возвращаясь
к описанию особенностей различных
подклассов граф-схем алгоритмов,
отметим, что для ГСА1 характерно,
что в них выдача значений выходных
переменных осуществляется не в
конце граф-схемы, а в любых
операторных вершинах.
ГСА1 могут
быть построены так, что в условных
вершинах применяются только
входные переменные типов X и T, а в
операторных вершинах — выходные переменные
типов Z и t, где T — переменные,
фиксирующие факт срабатывания
функциональные элементы задержки.
Наличие в ГСА1 только тех
переменных, которые упоминаются в
алгоритме управления, является
важным достоинством этого
подкласса граф-схем алгоритмов.
В ГСА2 крайне
редко используются только те
переменные, которые указаны в
алгоритме управления и не
применяются "лишние"
переменные. В качестве такого
примера на рис.3 приведена ГСА2,
реализующая R-триггер, в которой
используются только переменные,
определенные алгоритмом
управления: x1 — переменная
установки триггера; x2 — переменная сброса
триггера; z — выходная
переменная.
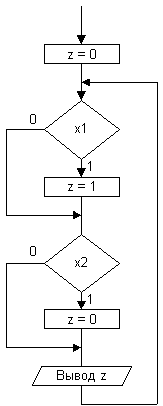
Рис. 3.
Даже эта граф-схема
алгоритма (без дополнительных
переменных) весьма трудно понимается,
так как выдача результатов в ней
происходит в конце тела программы и
поэтому при x1 = x2 = 1 значения z
вычисляются дважды (пересчитываются),
а кроме того в ней при x1 = x2 = 0
имеется "пустой" от
операторных
вершин путь, при прохождении
которого сохраняется предыдущее значение
z, что осуществляется за счет
запоминания во внешней
относительно граф-схемы
алгоритма ячейке памяти значений z,
указанных в операторных
вершинах.
Из
рассмотренного примера следует,
что если в ГСА2 существует хотя бы один
путь, при прохождении которого не
устанавливается ни нулевое, ни единичное
значение хотя бы одной выходной
переменной, то такая граф-схема реализует
последовательностный автомат и
однотактный - в противном случае.
Как
отмечалось выше, ГСА2 без "лишних"
переменных встречаются крайне редко.
В общем случае в этом подклассе
граф-схем алгоритмов в условных вершинах
наряду с входными переменными
типов X и T, проверяются также и значения
выходных переменных Z и
отсутствующие в алгоритме
управления промежуточные (внутренние)
переменные Y, которые
устанавливаются и сбрасываются
наряду с выходными переменными в
операторными переменными. В
силу того, что обычно используются
битовые переменные Y, то ГСА2 в этом случае
весьма громоздки. Кроме того они
обычно неупорядочены по структуре, так
как порядок расположения вершин и
их пометка в граф-схемах алгоритмов стандартами
не оговаривается. ГСА2 весьма
трудно понимаются и по причине применения
умолчаний сохраняющихся значений
переменных Y и Z.
ГСА2 также
трудно понимать в случаях, если
значения переменных зависят от
предыстории (значений
соответствующих переменных,
указанных в ранее расположенных
операторных вершинах), но их
особенно трудно читать,
если
значения переменных не только
зависят, но и изменяются в
соответствии с предысторией -
зависят от путей, по которым можно
попасть в рассматриваемую операторную
вершину. В последнем случае
возникают также большие проблемы с безошибочным
внесением изменений в граф-схемы.
Необходимо
отметить, что, если для
Программиста проверки переменных Y и Z
вполне естественны, а для
Разработчика объяснимы, то для
Заказчика, Оператора и Контролера
их наличие неприемлемо, так как,
например, Заказчик в техническом
задании обычно не просит
устанавливать какую-либо
внутреннюю переменную в единицу.
Особые сложности могут возникнуть
при чтении в тех случаях, когда
проверяемые переменные Y и Z одной
ГСА2 могут изменяться из
других
компонент алгоритма управления,
реализуемых в том же
вычислительном устройстве.
Из
изложенного следует, что если ГСА1 и
ГСА2 без проверки переменных Y и Z в
условных вершинах отражают только
семантику реализуемого алгоритма управления,
то ГСА2 с такими проверками
представляют собой алгоритм реализации
заданного алгоритма управления в
вычислительном устройстве, что делает
нецелесообразным использование
таких граф-схем в качестве языка общения.
Проблемы с
построением ГСА1 и ГСА2 на
изложенном не заканчиваются, так
как для безошибочного перехода к
граф-схеме программы и возможности проведения
экспертизы (для ответственных
объектов управления) желательно по
исходной граф-схеме алгоритма
построить ГСА3, учитывающую
основные свойства управляющих
конструкций используемого языка
программирования. Например, в
большинстве программируемых
логических контроллеров для команд
IF допустимы переходы только вперед
и запрещены возвраты назад. Другая
принципиальная особенность команд
IF многих логических контроллеров состоит
в том, что, во-первых, они
одноадресные, а, во-вторых, обладают тем
свойством, что если некоторая
команда IF при невыполнении условия передает
управление на команду (метку) CONT, то
тогда и все размещаемые
между
этими командами другие команды IF
при невыполнении условий также должны
передавать управление на
использованную метку CONT [34]. При
этом необходимо отметить,
что команда безусловного перехода
STOP позволяет реализовать
только внешнюю обратную связь.
В этих
условиях ГСА3 должна быть
линеаризованной и
структурированной только с помощью
управляющих конструкций "последовательное
соединение" и "неполный выбор".
В тех случаях, когда ГСА2 в исходном
виде обладает такой структурой (например,
рис.3), необходимость в построении
ГСА3 отпадает. Однако, если,
например, ГСА2, реализующая
однотактный автомат, описываемый булевой
формулой z = !x1x2 v x1!x2, имеет "плоскостную"
(рис.4), а не "линейную"
структуру, то для перехода к граф-схеме
программы и тексту программы по ней
целесообразно предварительно
построить ГСА3 (рис.5).
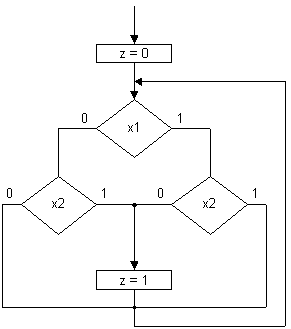
Рис. 4.
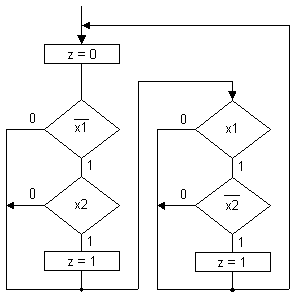
Рис. 5.
Из
рассмотрения последней граф-схемы
следует, что сложность ее понимания
по сравнению с ГСА2 (рис.4)
увеличилась (даже несмотря на то, что в
этих граф-схемах не используются
проверки переменных Y и Z), так как
при прохождении любого пути в ГСА3
входные переменные приходится проверять
неоднократно. При этом отметим, что
если программирование булевых формул
проводить не в бинарной, а в
операторной форме (непосредственно
по формуле), то ГСА2 всегда будет
иметь линейную структуру, что,
правда, в общем случае приводит к
снижению быстродействия и требует применения
промежуточных переменных.
В
вычислительных устройствах, в
которых ввод входных переменных может
осуществляться по мере
необходимости (как это имеет место
в некоторых типах программируемых
логических контроллеров), эти
переменные за один проход граф-схемы
алгоритмов могут не только
неоднократно проверяться, но и
изменять свои значения, что может
приводить к нарушению
функционального соответствия,
задаваемого спецификацией (таблицей
истинности), которое по аналогии с
аппаратной реализацией может быть
названо риском программной реализации.
Для уменьшения степени риска для
таких контроллеров должна использоваться
буферизация или применяться
максимально бесповторная реализация.
Таким
образом, если в ГСА1 отражается
только семантика реализуемого алгоритма
управления, в ГСА2 кроме семантики
учитывается возможность реализации
алгоритма управления, состоящего
из нескольких компонент, в одном вычислительном
устройстве, то в ГСА3 отражается
также специфика используемых
управляющих конструкций
применяемого языка
программирования. Однако ГСА3 еще
значительно отличаются от граф-схем
программ, так как в последних должна
отражаться также и семантика всех
используемых команд или
операторов
применяемого языка
программирования. При этом в граф-схемах программ
появляются упоминания о таких
архитектурных особенностях вычислительных
устройств, которые в исходной граф-схеме
алгоритма не используются.
Например, на рис.6 приведена граф-схема
программы, реализующая ГСА2 (рис.3),
в которой символом "БС"
обозначен битовый сумматор
программируемого логического
контроллера.
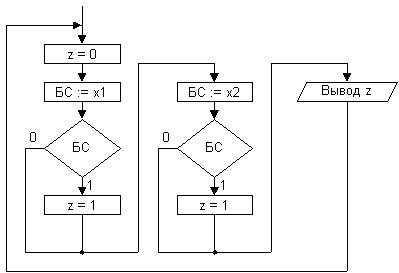
Рис. 6.
Из
изложенного следует, что граф-схемы
программ, а тем более тексты программ
не должны применяться в качестве
языка общения.
Поэтому
только ГСА1 без умолчаний могут
претендовать на роль языка общения,
однако при их программировании
возникают проблемы, связанные с их расцикливанием,
линеаризацией и структурированием.
Видимо, по этой причине на практике
обычно в лучшем случае строят ГСА2 и,
минуя построение других
граф-схем,
неформально пишут текст программы.
При этом
возникает проблема с выбором
тестов и доказательством правильности
программы, так как при таком
подходе из-за отсутствия "ясной" спецификации
не удается обсудить с
заинтересованными специалистами правильно
ли понята поставленная задача и
проблема "правильности" перекладывается
на испытания, при которых можно
обнаружить, что что-то делается
неправильно, но весьма трудно
обнаружить, что программа, в случае ошибок
в ней, может делать что-либо не
заданное спецификацией.
Эта проблема
усугубляется тем, что на практике
обычно методика проверки
функционирования представляет
собой таблицу, содержащую два столбца,
в первом из которых указываются
значения входных переменных, а во втором
— значения выходов.
Однако такая проверка,
естественная для однотактных
автоматов, некорректна для
последовательностных задач.
Создание же методики,
учитывающей также значения всех
внутренних, а в ряде случаев и
предшествующие значения выходных
переменных, при неупорядоченной структуре
граф-схем алгоритмов проблематично
из-за большой размерности.
По мнению
автора, весь этот клубок проблем во
многом связан с тем, что в граф-схемах
алгоритмов и программ и в
собственно программах обычно не
используется понятие "внутреннее
состояние" компоненты в целом, называемое
в дальнейшем "состояние", а
применяются лишь отдельные битовые переменные,
косвенно его характеризующие.
Введение этого понятия позволяет переходить
от граф-схем алгоритмов к графам
переходов и обратно и использовать
графы переходов в качестве языка
общения и спецификации.
3. Графы переходов.
Классификация
Определение
1. Граф переходов, в котором в
каждой вершине явно указаны значения
каждой выходной переменной,
назовем графом переходов автомата
Мура с явным заданием
значений всех выходных переменных.
В этом случае
значения выходов соответствуют
номеру вершины и не зависят от
предыстории. По этой причине такой
граф переходов просто понимается и в
него легко вносятся изменения.
Определение
2. Граф переходов, в котором в
вершинах, кроме явно определенных
значений одних переменных,
применяются также неявно, но однозначно
определенные значения других
переменных, назовем графом
переходов автомата Мура с
неявным заданием значений выходных
переменных.
Неявное
задание переменной в вершине
отображается прочерком, который в данном
случае может быть заменен только
одним значением булевой переменной. Эта
переменная в рассматриваемой
вершине сохраняет то значение,
которое присваивается ей во
всех "смежных" с ней вершинах.
Связь между двумя вершинами может
быть непосредственной с помощью
заходящей в вершину дуги или
транзитной через другие вершины, в
которых вместо значений этой переменной
используются проверки.
Графы
переходов этого типа читаются
несколько хуже, чем графы переходов автоматов
Мура первого типа, однако их
целесообразно использовать для сокращения
объема памяти программ, изоморфно
отражающих графы переходов автоматов
Мура. Графы переходов этого класса
могут быть изображены таким образом,
что в нем в каждой вершине в явном
виде указаны значения каждой выходной
переменной, а неизменяющиеся
относительно "смежных" вершин значения
этих переменных отмечаются
перечеркиванием.
Определение
3. Граф переходов, в котором в
вершинах, кроме явно определенных
значений одних переменных,
используются также неявно и
неоднозначно заданные значения
других переменных, назовем графом
переходов автомата Мура с
неоднозначным заданием значений
выходных переменных.
Графы
переходов этого класса могут
содержать для одной и той же задачи
меньшее число вершин, чем графы
переходов автоматов Мура двух
других указанных выше
разновидностей, так как в этом
случае в вершине вместо одного
значения умалчиваемой переменной
могут формироваться различные
значения той же переменной, что
порождает в этой вершине различные
наборы значений выходных
переменных и обеспечивает
эквивалентность одной такой
вершины нескольким, полностью
определенным.
Это
преимущество с точки зрения
компактности описания и сокращения
длины программы порождает
одновременно и главный недостаток
графов переходов этого типа — трудность их чтения и
понимания. Именно по этой причине
такие графы переходов не
рекомендуется использовать в
качестве языка общения.
Спецификацию
задач рассматриваемого класса
целесообразно производить с
помощью двух первых моделей графов
переходов автоматов Мура, а в
случае использования для
спецификации ГСА1 последнюю
целесообразно преобразовать к
одной из этих моделей графов
переходов.
Это,
естественно, не исключает
применение графов переходов для
других классов автоматов.
Аналогичная классификация может
быть предложена для графов
переходов автоматов Мили, в которых
значения выходных переменных
формируются не в вершинах графов
переходов, а на дугах [36]. Во многих
задачах логического управления
переход от модели автомата Мура к
модели автомата Мили не уменьшает
числа состояний (вершин графа
переходов). На рис.7 в качестве
примера приведен граф переходов
автомата Мура, реализующий счетный
триггер, а на рис.8 эта же задача
описана с помощью графа переходов
автомата Мили.
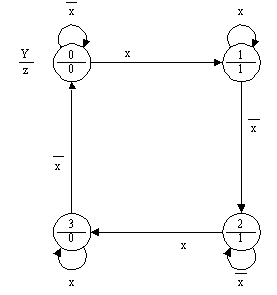
Рис. 7.
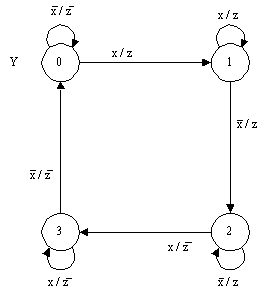
Рис. 8.
В других
случаях переход от графа переходов
автомата Мура или графа переходов
автомата без выходного
преобразователя к графу переходов
автомата Мили позволяет сократить
число вершин. На рис.9 приведен граф
переходов автомата без выходного
преобразователя с четырьмя
вершинами, реализующий
последовательностный
одноразрядный сумматор, а на рис.10
этот алгоритм описан графом
переходов автомата Мили с двумя
вершинами.
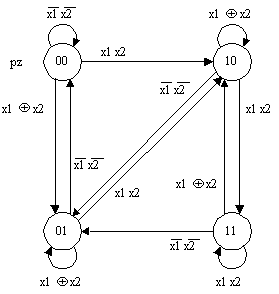
Рис. 9.
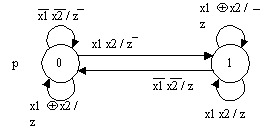
Рис. 10.
При этом
необходимо отметить, что если для
автоматов Мура и автоматов без
выходного преобразователя с
однозначным заданием значений
выходов число состояний равно
числу комбинаций этих значений (среди
которых учитываются повторяющиеся),
а для автоматов, в которых все
комбинации различны, равно числу
различных комбинаций, то уже для
автоматов этих классов с
неоднозначным их заданием понятие
"состояние" становится менее
связанным со значениями выходов и
поэтому становится более
абстрактным и менее понятным.
Это
положение усугубляется для
автоматов Мили, а для автоматов
этого класса с неоднозначными
значениями выходов в [37] вместо
понятия "состояние" было
введено понятие "ситуация", а
вместо термина "граф переходов" — термин
"граф переключений". Однако
несмотря на то, что граф
переключений может содержать
меньшее число вершин, чем
эквивалентный граф переходов,
применение графов переключений в
качестве языка общения
нецелесообразно ввиду сложности их
понимания.
Аналогичная
ситуация с числом состояний из-за
умолчаний значений переменных
может иметь место и для такого типа
автоматов как смешанные автоматы — "автоматы без
выходного преобразователя-Мили (СА1)"
и "автоматы Мура-Мили (СА2)", а
также для автоматов всех
перечисленных классов с флагами, в
которых одна и та же переменная
может использоваться в одном графе
переходов как в качестве входной,
так и выходной переменной.
В качестве
флага в ряде случаев могут
использоваться переменные, если
они находятся в ячейках памяти,
значения которых проверяются
автоматом и могут быть изменены не
только внешним относительно
рассматриваемого автомата
источником информации, например
кнопкой, но и собственно автоматом.
В графе переходов СА2 (рис.11) в
качестве флага используется
переменная x1, значения которой,
сохраняемые во внешней
относительно автомата битовой
ячейке памяти, могут быть изменены
в устойчивых состояниях автомата
кнопкой или собственно автоматом
на переходе 0-2, инициируемом
входной переменной x0. Значения
переменной x1 не только формируются
автоматом, но и проверяются им на
переходах 0-1 и 2-3.
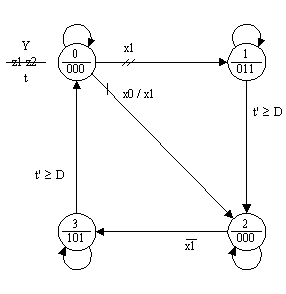
Рис. 11.
Более
типично использование флагов как
дополнительно введенных
переменных, которые воздействуют
на ячейки памяти, содержимое
которых не может быть изменено от
других источников информации. В
случае, когда флаги вводятся в
автомат без выходного
преобразователя, то эти ячейки
могут рассматриваться как
принадлежность автомата наряду с
ячейками, сохраняющими значения
переменных, различающих состояния.
Для
автоматов Мура, Мили и смешанных
автоматов флагами являются
дополнительно вводимые переменные
F, значения которых запоминаются в
ячейках памяти, внешних
относительно рассматриваемого
автомата. Если при использовании
многозначного кодирования
состояний автомата любой сложности,
принадлежащих этим классам,
достаточно иметь в автомате только одну
промежуточную переменную, то при
введении флагов во внешней
относительно автомата среде
появляются дополнительные ячейки
памяти, в том числе и многозначные.
При этом номер следующего
состояния определяется не только
номером рассматриваемого
состояния и входным воздействием,
как это имеет место в автоматах без
флагов, но зависит от предыстории.
Таким
образом, для таких автоматов не
только значения выходов, но и
значения состояний могут зависеть
и изменяться от предыстории, что,
естественно, резко усложняет их
чтение.
На рис.12
приведен не содержащий ни одной
устойчивой вершины граф переходов
автомата Мура с десятью вершинами.
Число вершин в графе переходов
автомата Мура удается сократить до
семи за счет введения двоичного
флага F1, формируемого и
проверяемого автоматом, и
неоднозначности значений флага в
некоторых вершинах графа переходов
(рис.13). Дальнейшее сокращение числа
вершин в графе переходов автомата
Мура обеспечивается введением
дополнительного многозначного
флага F2 и использованием умолчаний
его значений (рис.14).
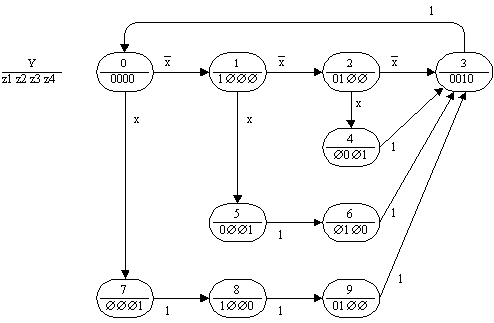
Рис. 12.
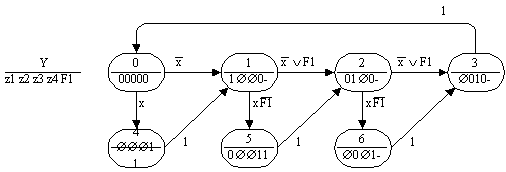
Рис. 13.
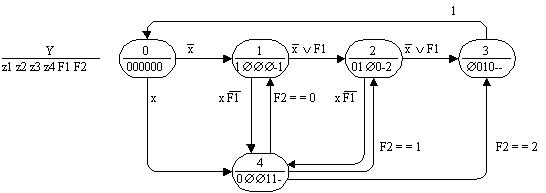
Рис. 14.
Методы
построения понимаемых графов
переходов по граф-схемам
алгоритмов и понимаемых граф-схем
алгоритмов по графам переходов, а
также методы программирования
рассматриваемых моделей в базисе
языков различных уровней
рассматриваются во второй части
работы.
СПИСОК ЛИТЕРАТУРЫ
| 1. |
Требования
к спецификации программ /Под
ред. Агафонова В.Н. М.: Мир, 1984. |
| 2. |
Клини С.
Представление событий в
нервных сетях и конечных
автоматах //Автоматы. М.: Изд-во
иностр. лит, 1956. С.17-27. |
| 3. |
Ляпунов
А.А. О логических схемах
программ //Проблемы
кибернетики. М.: Физматгиз, 1958.
Вып.1. С.5-28. |
| 4. |
Янов Ю.И.
О логических схемах алгоритмов
//Проблемы кибернетики. М.:
Физматгиз, 1958. Вып.1. С.29-53. |
| 5. |
Калужнин
Л.А. Об алгоритмизации
математических задач //Проблемы
кибернетики. М.: Физматгиз, 1958.
Вып.1. С.58-63. |
| 6. |
Таль А.А.
Анкетный язык и абстрактный
синтез минимальных
последовательностных машин //Автоматика
и телемеханика (А и Т). 1964. N 6. С.38-49. |
| 7. |
Гаврилов
М.А., Девятков В.В., Чичковский А.Б.
Язык операторных схем
параллельных алгоритмов с
памятью (язык ОСПАП) //Абстрактная
и структурная теория релейных
устройств. М.: Наука, 1975. С.18-30. |
| 8. |
Глушков
В.М., Капитонова Ю.В.,
Летичевский А.А. О применении
метода формализованных
технических заданий к
проектированию программ
обработки структур данных //Программирование.
1978. N6. С.5-12. |
| 9. |
Кузнецов
О.П. Теория алгоритмических
конечноавтоматных языков //А и
Т. 1981. N 3. С.122-133. N4. C.127-135. |
| 10. |
Кузнецов
О.П., Шипилина Л.Б., Марковский А.В.
и др. Проблемы разработки
языков логического
программирования и их
реализация на микро - ЭВМ (на
примере языка ЯРУС - 2) //А и Т. 1985.
N 6. С.128-138. |
| 11. |
Девятков
В.В., Чичковский А.Б. Условие-82 -
язык программно-логического
управления //Автоматизация
проектирования. М.:
Машиностроение, 1990. Вып.2. С.58-67. |
| 12. |
Амбарцумян
А.А., Искра С.А., Кривандина Н.Ю. и
др. Проблемно-ориентированный
язык описания поведения систем
логического управления ФОРУМ-М
//Проектирование устройств
логического управления. М.:
Наука, 1984. С.35-47. |
| 13. |
Юдицкий
С.А., Покалев С.С. Логическое
управление гибким
интегрированным производством.
Препринт. М.: Ин-т проблем
управления, 1989. |
| 14. |
Закревский
А.Д. Языки логического
управления. Препринт. Минск: Ин-т
технической кибернетики, 1988. |
| 15. |
Лазарев
В.Г., Пийль Е.И. Синтез
управляющих автоматов. М.:
Энергоатомиздат, 1989. |
| 16. |
Баранов
С.И. Синтез микропрограммных
автоматов (граф-схемы и
автоматы). Л.: Энергия, 1979. |
| 17. |
Флорин
Ж. Таблицы этапов или сети
Петри? //Теория дискретных
управляющих устройств. М.:
Наука, 1982. С.35-42. |
| 18. |
Захаров
В.Н. Секвенциальное описание
управляющих автоматов //Изв. АН
СССР. Техн.кибернетика. 1972. N2. С.58-65. |
| 19. |
Фрайтаг
Г.,Годе В., Якоби Х. и др.
Введение в технику работы с
таблицами решений. М.: Энергия,
1979. |
| 20. |
Базиль
Д. Реализация конечного
автомата на языке Форт //Форт в
исследованиях и разработках. Л.:
Ленинградский гос. ун-т, 1991. Т.1. N1.
С.5-8. |
| 21. |
Сосье Г.
Управляющие автоматы:
моделирование, декомпозиция и
реализация. //Теория дискретных
управляющих устройств. М.:
Наука. 1982. С.49-58. |
| 22. |
Бардзинь
Я.М., Калниньш А.А., Стродс Ю.Ф. и
др. Язык спецификации SDL и
методика его использования.
Рига: Латвийский гос. ун-т. 1986. |
| 23. |
Бергер
Г. Программирование
управляющих устройств на языке
STEP 5. SIEMENS, 1982. |
| 24. |
Мишель
Ж. Программируемые контроллеры.
Архитектура и применение. М.:
Машиностроение, 1992. |
| 25. |
Шалыто
А.А. Программная реализация
управляющих автоматов //Судостроительная
промышленность. Сер.
Автоматика и телемеханика. 1991.
Вып.13. С.41-42. |
| 26. |
Шалыто
А.А. Технология программной
реализации алгоритмов
логического управления как
средство повышения живучести //Тез.
докл. научно-технической конф."Проблемы
обеспечения живучести
кораблей и судов". СПб.:
Судостроение, 1992. С.87-89. |
| 27. |
Котов В.Е.,
Сабельфельд В.К. Теория схем
программ. М.: Наука, 1991. |
| 28. |
Ершов А.П.
Введение в теоретическое
программирование. М.: Наука, 1977. |
| 29. |
Схемы
алгоритмов, программ, данных и
систем. Условные обозначения и
правила выполнения. ГОСТ 19.701-90 (ИСО
5807-85). |
| 30. |
P -
схемы алгоритмов и программ.
ГОСТ 19.005 - 85. |
| 31. |
Иодан Э.
Структурное проектирование и
конструирование программ. М.:
Мир, 1979. |
| 32. |
Лингер
Р., Миллс Х., Уитт С. Теория и
практика структурного
программирования. М.: Мир, 1982. |
| 33. |
Буч Г.
Объектно - ориентированное
проектирование с примерами
применения. Киев: Диалектика,
1992. |
| 34. |
Al 2000.
Technical Description. FF-ELEKTRONIIKKA FREDRIKSSON KY,
1992. |
| 35. |
Вирт Н.
Программы = алгоритмы + данные.
М.: Мир, 1988. |
| 36. |
Брауэр
В. Введение в теорию конечных
автоматов. М.: Радио и связь, 1987. |
| 37. |
Кузнецов
О.П. Графы логических автоматов
и их преобразования. //А и Т. 1975. N9.
C.118-129. |
[ Часть 2 ]
|