Крылья, ноги и хвосты

Можно скачать текст статьи в формате html (50 кб)
Примеры программ к статье (3,2 кб)

© 2002 г. А. И. Легалов

Написание этой статьи было "спровоцировано" публикацией [1], посвященной использованию автоматного программирования для распознавания входных цепочек, принадлежащих заданным языкам. Думаю, что тесное сосуществование с авторами в едином информационном пространстве [2] показывает мое положительное отношение к их идеям. Однако конкретное решение вполне определенных примеров навело на размышления о связи моделей, методов и классов задач, которыми хотелось бы поделиться.

Хвост

Каждая конкретная задача инициирует поиск определенных методов ее решения. Зачастую, одно и то же решение можно получить несколькими путями, особенно, если условие является достаточно простым. Бывает, что сама постановка задачи показывает, как ее реализовать, а предварительный анализ, проводимый до написания программы, позволяет получить универсальное решение. В работе [1], обобщение задачи оказалось в самом хвосте, так как в основе лежала демонстрация автоматных концепций. Поэтому, на мой взгляд, в данном конкретном случае, произошла некоторая "недооценка" в использовании счетчика.

Рассмотренные в статье языки порождают простые цепочки по одному общему закону: осуществляется подсчет одинаковых символов, стоящих в голове, а затем определяется совпадение их числа для каждой из групп символов, определяющих хвост. В целом не важен состав этих символов и порядок их следования. Главное, чтобы за подцепочкой из n одних символов следовала подцепочка из стольких же, но других символов.

Условие подобной задачи можно описать и без использования формальных грамматик. Дано множество символов A = {a₁, a₂, ..., a_k}, размещенных на "входной ленте". Принадлежность цепочки к некоторому языку L определяется в том случае, если цепочка C имеет вид:

C = ... a_iⁿ a_jⁿ ... ,

где a_i не равно a_j для любых рядом стоящих групп символов. Допускаются цепочки, состоящие только из одной группы символов, т.е., с пустым хвостом.

Это условие можно использовать для построения обобщенного автомата. Однако оно вполне может служить отправной точкой и для написания программы с применением структурного программирования, столь популярного в 70-х годах прошлого столетия:

1. Прочитать с ленты первый символ и подсчитать, сколько раз подряд он встретится.
2. При изменении символа зафиксировать подсчитанное количество в переменной X.
3. Для каждой из последующих групп символов осуществлять их подсчет и сравнение с X. Если значения не совпадают, то выдать сообщение об ошибке и закончить программу.
4. При совпадении символов во всех группах и завершении входной цепочки выдать сообщение об ее допуске.

Соответствующий фрагмент программы, допускающей отсутствие хвоста, может выглядеть следующим образом:

// Подсчет встречаемости первого символа
int FirstCounter(tape &t) {
  int counter = 0;      // количество символов
  t.First();            // установка ленты на первый символ
  char c = t.Read();    // его значение
  if(c=='\0') return 0; // в случае пустой строки
  do {
    counter++;
    t.Next();           // сдвиг на следующий символ
  } while(c == t.Read());
  return counter;       // возврат числа символов
}

// Подсчет символов в следующих после головы группах
int NextCounter(tape &t) {
  int counter = 0;
  char c = t.Read();
  if(c=='\0') return 0;
  do {
    counter++;
    t.Next();
  } while(c == t.Read());
  return counter;
}

// Разбор произвольной цепочки, возможно, с пустым хвостом
bool common_parser(tape &t) {
  // Подсчет символов в голове
  int counter = FirstCounter(t);
  if(counter == 0) return false; // пустая голова
  // Подсчет символов в хвостах
  while(t.Read() != '\0') {
    int tail_counter = NextCounter(t);
    // Проверка на различное число символов
    if(counter != tail_counter) return false;
  }
  return true;
}

При желании, можно обратиться к конструктивизму, и "разбавить" программу ОО штучками, столь популярными в конце предыдущего и начале нынешнего века. Их использование позволяет инкапсулировать механизм реализации ленты.

// Абстрактная лента. Переопределяется в дальнейшем
class tape {
public:
  // Установить головку на первый символ.
  virtual void First() = 0; 
  // Установить головку на следующий символ.
  virtual void Next() = 0; 
  // Прочесть текущий символ.
  // Читает \0, если символ отсутствует.
  virtual char Read() = 0; 
};

В дальнейшем можно безболезненно подставлять тот вид ленты, который нужен в контексте решаемой задачи. Например, используем строку символов:

// Лента на основе строки символов
class string_tape: public tape {
public:
  void First() { _i = 0; } 
  void Next()  { ++_i; }
  char Read()  { return _s[_i]; }
  // Конструктор
  string_tape(string s): _s(s), _i(0) { }
private:
  string _s; // хранение символов входной цепочки
  int _i;    // индекс текущего элемента
};

Использование распознавателя не вызывает особых проблем:

// Тестовая функция
void main() {
  tape *t;
  cout << "common_parser testing" << endl;
  t = new string_tape("aaafffsssqqqwww");
  if(common_parser(*t)) cout << "Chain is correct!" << endl;
  else cout << "Chain is bad!" << endl;
  delete t;
  // И далее различные варианты теста...
}

Программу можно легко свести к виду, обеспечивающему анализ любых ограниченных цепочек, состоящих из групп символов одинаковой длины. Надо просто добавить фильтр, регламентирующий появление заданных символов. Получим ограничивающий распознаватель:

// Разбор цепочки с заданной последовательностью символов
// Если шаблон пуст, то осуществляется произвольный разбор
bool limited_parser(tape &t, string s="") {
  // Проверка на значимость строки символов
  if(s=="") common_parser(t); // общий разбор
  else { // разбор по шаблону
    // Проверка головы на соответствие шаблону
    t.First();
    if(s[0] != t.Read()) return false; // не та голова
    // В противном случае начинаем разбор головы
    int counter = FirstCounter(t);
    if(counter == 0) return false; // пустая голова
    // Подсчет символов в хвостах
    int i = 1; // индекс текущего шаблона хвоста
    while(t.Read() != '\0') { // хвост существует
      if(s[i] != t.Read()) return false; // не тот хвост
      int tail_counter = NextCounter(t);
      // Проверка на различное число символов
      if(counter != tail_counter) return false;
      i++; // следующий шаблонный элемент
    }
    // Проверка на перебор всего шаблона
    if(i != s.length()) return false;
  }
  return true;
}

К сожалению, стремление воспользоваться уже написанными функциями привело к дублированию проверок первых элементов каждой из групп символов входной цепочки. Эта проблема легко устранима, и для демонстрационной программы не является существенной. Однако, следует подчеркнуть, что подобная ситуация весьма характерна для традиционного программирования. Тестовый фрагмент можно добавить в ранее написанную главную функцию:

// Что-то было...
cout << "limited_parser testing" << endl;
t = new string_tape("111000111000111");
if(limited_parser(*t, "10101")) 
  cout << "Chain is correct!" << endl;
else 
  cout << "Chain is bad!" << endl;
delete t;
// Что-то будет...

Написание программы показывает, что более тщательный предварительный анализ задачи и, возможно, ее обобщение могут привести к простым и очевидным решениям, позволяющим не вспоминать о теориях. Достаточно бывает опереться на базовые знания, впитываемые с изучением основ программирования. Заодно, хотелось бы обратить внимание, что, кроме алгоритмических проблем, решаемых теориями формальных грамматик и автоматов, необходимо постоянно помнить и об эмпирических методах конструирования абстракций, адекватно отражающих описываемые понятия. В противном случае, никакая теория не поможет в дальнейшем безболезненном расширении функциональных возможностей.

Ноги

Несомненно, что увеличение сложности программы ведет к трудностям в ее разработке "естественным" путем. Косвенно это подтверждает и написание функции ограниченного распознавателя: распределенное вложение одних условий в другие не улучшает понимание исходного текста. Проблема заключается в том, что равноправие между операторами императивного языка, вытекающее из особенностей фон-неймановской архитектуры, приводит к смешению логики управления и вычислительных операций. Применение специализированных моделей организации команд и данных позволяет структурировать решение и разделить концептуально отличающиеся процессы

Конечные автоматы отделяют логику управления от вычислительных функций, что позволяет облегчить разработку программ за счет разделения этих абстракций. Правда, в своей трактовке рассматриваемого вопроса, я бы не стал опираться на машину Тьюринга, для обоснования их преимуществ. На мой взгляд, ноги современных прикладных решений растут из машины Фон Неймана, обеспечивающей платформу для построения программ, эмулирующих разные модели, включая и конечны автоматы (рис. 1).

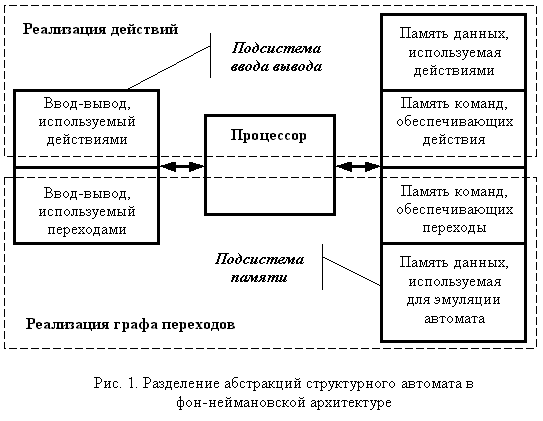
Действия автоматов отделены от логики переходов и используются для модификации данных, размещенных в рабочей памяти. Некоторые из этих данных могут участвовать в организации логики управления. Часть памяти используется для эмуляции переходов самого автомата. Точно таким же образом могут разделяться и устройства ввода-вывода.

Вместе с тем модели, ориентированные на определенные предметные области, формируют свое восприятие задачи, которое часто обеспечивает большую наглядность по сравнению с моделями, используемыми в этих областях "случайно". Разработка распознавателей цепочек также базируется на автоматах, содержащих входную ленту, устройство управления с конечной памятью, рабочую память [3]. Структура этого автомата представлена на рис. 2. Следует отметить, что лента распознавателя используется не так, как лента машины Тьюринга.

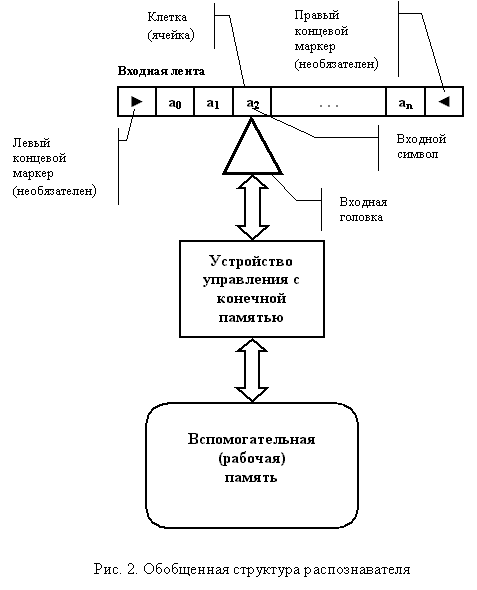
Приведенное на рисунке устройство управления с конечной памятью является обычным конечным автоматом и задается графом переходов, представленным в нижней части рис. 1. На ленте и вспомогательной памяти стоит остановиться подробнее. В отличие от обычного автомата, действия которого на уровне модели смотрятся одинаково, лента и вспомогательная память используются для представления специфических устройств. Выделение этих дополнительных понятий позволяет специализировать модель и формализовать ее использование в конкретной предметной области - только при анализе цепочек. Это, в свою очередь, повышает эффективность построения распознавателей. В представленном автомате отсутствует память, предназначенная для реализации других действий, например, семантической обработки или генерации кода. Считается, что она выбирается по усмотрению разработчика.

Использование формальных грамматик для описания языков обеспечивает процесс разработки дополнительной инструментальной поддержкой: убираются лишние детали в ходе проектирования. Взаимосвязь между конкретными классами грамматик и автоматов позволяет формально перейти от описания языков к соответствующей модели распознавателя. Выделение различных классов грамматик позволяет сориентироваться на реализации тех языков, которые необходимы разработчику. Например, использование контекстно-свободных (КС) грамматик позволяет формировать только иерархические и рекурсивно вложенные отношения между понятиями. Контекстно-зависимые (КЗ) грамматики обеспечивают описание более сложных отношений. Вполне естественно, что для распознавания ограниченных языков целесообразнее использовать и ограниченную грамматику, определяющую специализированный и более эффективный автомат, а не стремиться покрыть одним автоматом множество всех вариантов. В этом случае можно сразу обратиться к машине Фон Неймана. Формальные грамматики являются моделью, стоящей над различными автоматными моделями для увеличения уровня абстракции при решении прикладных задач конкретного класса.

Подобный же прием используется в [1] для перехода от модели автомата к тексту программы, написанной с применением switch-технологии. Сама автоматная модель, содержащая счетчик символов и прочие "украшения", построена тем же эвристическим приемом, каким воспользовался я при непосредственном создании процедурной версии. Усложнение условия решаемой задачи приведет к неминуемому поиску новых частных эвристик и их неформализованному включению. В конце концов, встанет тот же вопрос: переходить ли к использованию моделей, повышающих уровень абстракции и стоящих над моделью структурного автомата или продолжать "естественные мучения", характерные при использовании выбранного подхода в несвойственной ему предметной области?

Следует отметить, что, для повышения уровня абстракции и упрощения процесса разработки, не обязательно над одной моделью выстраивать другую. Можно "обойтись" созданием соответствующих методик. В теории управления наработано множество приемов, позволяющих провести разбиение и упрощение решаемой задачи перед тем, как "положить" ее на автоматную модель. Поэтому, в этой области switch-технология достигла определенных успехов [2].

Теория языков тоже достаточно далеко подвинулась в установлении связей с автоматами, обеспечивающими реализацию. Появление атрибутных транслирующих грамматик [4] способствовало включению механизмов работы с выходной лентой. Неплохо формализован и семантический разбор. Во многом, только отсутствие надлежащего уровня знаний в специфических предметных областях заставляет искать нас собственные эвристики.

Общеизвестно, что для одних и тех же классов грамматик могут быть использованы различные распознаватели. Например, КС грамматики можно распознавать не только автоматами со стековой памятью, но и множеством динамически порождаемых конечных автоматов [5], опирающихся на рекурсивный спуск. Их эквивалентность вытекает из того, что вызовы функций в современных языках реализуются через стек. В [5] можно посмотреть, как распознаватели вложенности скобок реализованы с использованием как автомата с магазинной памятью, так и с помощью динамически порождаемых конечных автоматов.

Можно легко показать, что любая величина моделируется конечным число ячеек памяти, хранящим "палочки", соответствующие ее значению, конечную память можно описать эквивалентным конечным автоматом без рабочей памяти. Любая изменяющаяся величина моделируется через динамически меняющуюся память (стек - один из вариантов), динамическая память заменяется динамически порождаемыми конечными автоматами. Не существует проблем в определении эквивалентности системы, использующей простой набор команд, оперирующих с произвольной памятью, и модели, реализующей аналогичное решение с помощью клеточных автоматов или рекурсивных функций. В компьютерной философии это уже давно определено тезисом Черча. Как следствие - отсутствие четкой границы между памятью и алгоритмическими методами имитации памяти, алгоритмами и табличными методами получения решения.

Обратившись к задаче, фигурирующей в качестве примера, следует отметить, что автомат со счетчиком можно без проблем заменить автоматом, содержащим два стека. Условием допуска, в этом случае, будет пустота одного стека при заполненном другом. Аналогичное решение можно получить, если воспользоваться только конечными автоматами, взаимодействующими по принципу сопрограмм, широко применяемому в языках программирования Модула-2 [6] и Симула-67 [7]. Поэтому, вряд ли стоит говорить об универсальности и большей эффективности исходного решения при распознавании рассматриваемых цепочек. Предложенные варианты не будут сложнее. Они лишь будут решать задачу другими методами.

Крылья

Руководствуясь при покупке удобством упаковки, мы порой не замечаем, что пьем из одной бочки. Окрыленные любимыми идеями, моделями, инструментами и прочей символикой, мы с энтузиазмом используем их в реализации поставленных задач. Но в каждой предметной области возникают "смежные и небольшие" проблемы, требующие несколько иного решения. В подобных ситуациях смело, и вполне обоснованно, делаются попытки применить хорошо освоенные навыки в несвойственной сфере. Для этого есть следующие пути:

1. Взяв за основу универсальный инструмент (модель) можно "заточить" его под нестандартное решение. Такую настройку можно осуществлять каждый раз, когда возникнет аналогичная ситуация. В результате будет накоплен комплект, пригодный для повторного использования в аналогичных ситуациях. Именно этот путь, на мой взгляд, и предложен в [1], что позволило использовать универсальную концепцию автомата в более специфических приложениях.

2. Можно пойти от противного: если инструмент невозможно использовать, то надо попытаться "разобрать заготовку" и произвести с ней необходимые манипуляции. После этого, используя клей, гвозди, винты и хомуты, собрать все как было. Несмотря на внешнюю "топорность" этого варианта, он успешно применяется в программировании, что я и хотел бы продемонстрировать рядом примеров.

Рассмотрим весьма частный случай формирования длинной целочисленной константы в языке программирования C++. Ее, например, можно описать следующим образом:

  
const long int A = 10;

Однако, это не единственный вариант. Возможны также:

  
const A = 10; int const A = 10; и т.д.

Более общее описание типов выглядит в C++ еще разнообразнее. Однако, даже для рассматриваемого случая КС правило, приведенное на рис. 3 с использованием диаграмм Вирта, смотрится громоздко.

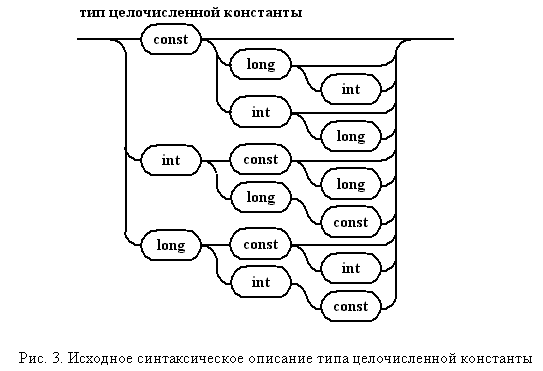
"Разборка" заключается в упрощении диаграммы Вирта путем зацикливания трех используемых ключевых слов. Это обеспечивает порождение цепочек, состоящих из const, long, int, следуемых в произвольном порядке, и в любом количестве. Для того чтобы "скрепить" правило, необходимо добавить код, подсчитывающий частоту встречаемости каждого ключевого слова. Перед выходом из правила нужно проанализировать накопленную комбинацию ключевых слов. Измененное правило представлено на рис. 4. В выносках обозначены выполняемые семантические действия.

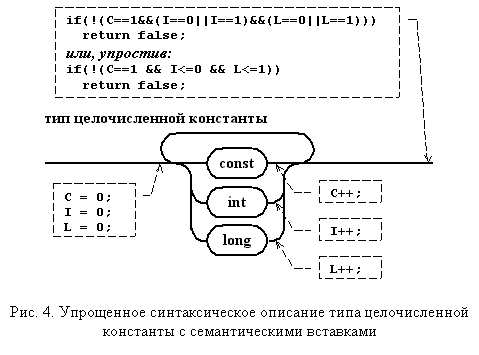
Подобный прием пригоден не только для упрощения грамматики, но и для изменения ее вида. В частности, КЗ-грамматику можно заменить контекстно-свободной, расширяющей число цепочек, порождаемых языком. Ограничитель реализуется путем семантических вставок. Перепишем пример со счетчиком еще одним способом. Чтобы уменьшить объемы рассуждений и программы, остановлюсь только на распознавателе цепочек языка {1ⁿ0ⁿ1ⁿ | n > 0}.

Правило, определяющее "обрубленный" каркас выглядит следующим образом (рис. 5):

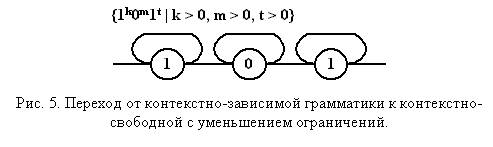
Оно распознает множество цепочек вида: {1^k0^m1^t | k > 0, m > 0, t > 0}. Введем счетчик символов в головной группе. Их число в каждой последующей группе будет определяться соответствующей переменной n (рис. 6). Следует отметить изменение правила, в котором отдельно выделено распознавание первых символов. Это обусловлено отличием семантической обработки для начала и продолжения группы. Дополнительной разметкой указаны точки анализа символов входной цепочки.

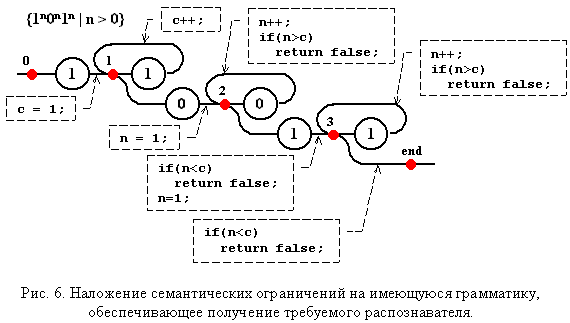
Ниже приводится функция, механически построенная по этой диаграмме. Ее ретроградный вид обосновывается в [5].

  
// Сделать разбор цепочки: 101,
bool parser_101(tape &t) {
//_0:
  int c;     // счетчик символов в голове
  int n;         // счетчик символов для каждой из групп хвоста
  t.First(); // установка в начало цепочки
    // Разбор в начальной точке
    if(t.Read()=='1') {c=1; t.Next(); goto _1;}
    return false;
_1: // Продолжить разбор головы или взять второй символ 
    if(t.Read()=='1') {c++; t.Next(); goto _1;}
    if(t.Read()=='0') {n=1; t.Next(); goto _2;}
    return false;
_2: // Продолжить разбор второй группы или взять символ третьей группы 
    if(t.Read()=='0') {
      n++; 
      if(n > c) return false;
      t.Next(); goto _2;
    }
    if(t.Read()=='1') {
      if(n < c) return false;
      n=1; 
      t.Next(); goto _3;
    }
    return false;
_3: // Разбор последней группы или выход
    if(t.Read()=='1') {
      n++; 
      if(n > c) return false;
      t.Next(); goto _3;
    }
    if(n < c) return false;
    goto _end; // выход на конец по любому другому символу
_end:
    // Проверка на окончание цепочки
    if(t.Read()!='\0') return false;
    return true;
}

Конечно, представленный подход не так формализован, как switch-технология, но я успешно его использую уже более десяти лет.

Тело

Таким образом, существует, по крайней мере, два пути "улучшения" используемых моделей под свои нужды. Каждый обладает своими достоинствами и недостатками.

"Расширение номенклатуры инструментов" позволяет достаточно просто понятно и "до бесконечности" получать требуемые эффекты. Необходимо только, время от времени, подыскивать необходимые эвристики. Не нужно дополнительных знаний для выяснения: где "заточить", а где "подпаять" или "довинтить". К недостаткам можно отнести несколько бессистемное формирование комплекта расширений, избыточность и дублирование их свойств, трудности совместной стыковки при решении более общей задачи, требующей согласованного использования порознь наработанных отдельных "заточек". Изменение базовых концепций может привести к бесполезности и выбросу на свалку всего комплекта используемых инструментов. Подобная участь постигла, например, библиотеку "Object Windows Library" (OWL) при смене компанией Borland концепций разработки. Скорее всего, в ближайшее время, "за ненадобностью", под давлением .NET, исчезнет и библиотека MFC (Microsoft Foundation Classes).

Использование ограниченных моделей требует их предварительного изучения, что ведет к неоправданным временным и, особенно, интеллектуальным затратам. Очень часто такую модель приходится дополнительно расширять и обобщать, чтобы решить реальную задачу. Однако, опора на модели, стоящие над конкретными парадигмами и инструментами позволяет иметь достаточно консервативный теоретический базис, многократно используемый на уровне общих концепций. Переход к более низкому программному уровню в большинстве случаев осуществляется автоматически или, в крайнем случае, механически. Это подтверждается многолетним применением, как теории формальных грамматик, так и теории автоматов.

Следует также отметить, что в реальной разработке вряд ли стоит отдавать явное предпочтение одному из методов. Для того чтобы успешно продвигать продукт, нужно разливать его в разные тары. Оба представленных подхода дополняют друг друга, и являются составными частями процессов восходящего и нисходящего проектирования.

В этом клубке противоречий самым неожиданным образом переплетаются отношения между подходами, обеспечивающими переход, как от частного к общему, так и от общего к частному. Теория автоматов является тому наглядным примером. На ее основе, практически без программирования, можно создавать работающие программы в ряде специфических областей. Она же является основой для создания не только программ, но и узкоспециализированных моделей, порождаемых спецификой решаемых задач. Поэтому, дальнейшее развитие и популяризация этого направления должны благоприятно отразиться на повышении общей культуры разработки программного обеспечения.

Однако, существует огромное число задач, при решении которых естественным является использование других методов и парадигм, более адекватно отображающих используемые абстракции. Разнообразные модели, парадигмы, методы и методологии бренным телом "ложатся" на фон-неймановскую архитектуру в виде соответствующих инструментов. При замене этой архитектуры на любую другую телесная оболочка будет полностью перенесена, так как именно она определяет существование множества абстракций и принципов их выделения. Вот только небольшой срез параметров, учитываемых при написании программ: способы компоновки программных объектов, методы написания кода, методы типизации, управление параллельными вычислениями и многое, многое другое.

Литература

1. Шалыто А.А., Туккель Н.И. От тьюрингова программирования к автоматному. Мир ПК, № 2, 2002.

2. Сайт http://www.softcraft.ru/.

3. Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. В 2-х томах. - М.: Мир, 1978.

4. Льюис Ф., Розенкранц Д., Стирнз Р. Теоретические основы проектирования компиляторов. - М.: Мир, 1979.

5. Легалов А.И. Основы разработки трасляторов. Конспект лекций. - Размещены по адресу: http://www.softcraft.ru/translat/lect/.

6. Вирт Н. Программирование на языке Модула-2: Пер. с англ. - М.: Мир, 1987. - 224 с.

7. Андрианов А.Н., Бычков С.П. Хорошилов А.И. Программирование на языке Симула-67. - М.: Наука, 1985. - 288 с.

Написана в апреле-мае 2002 года