|
В. C. Любченко
Задача Эдсгера В. Дейкстры о пяти обедающих философах (см. [1,2]) одна из самых известных задач, на примере которой демонстрируют и изучают различные проблемы описания и функционирования параллельных систем. Особенность приведенного далее решения состоит в том, что получено оно на базе модели, которую часто необоснованно отвергают, как формальный инструмент описания параллельных систем. Иногда просто под влиянием достаточно распространенного "мнения" о том, что конечные автоматы не подходят для описания систем параллельного типа. Если уж не развенчать, то значительно его поколебать его нам поможет приведенное далее "автоматное решение" задачи Дейкстры о философах.
Формулировка задачи
В одном пансионе, открытом богатым филантропом, были собраны пять знаменитых философов[2]. Предаваясь размышлениям, они независимо друг от друга заходили обедать в общую столовую. В столовой стоял стол, вокруг которого был поставлены стулья. Каждому философу свой стул. Слева от философа лежало по вилке, а в центре стола стояла большая тарелка спагетти. Спагетти можно было есть только двумя вилками, а потому, сев за стол, философ должен был взять вилку соседа справа (если она, конечно, свободна).
Кроме проблемы создания модели такой системы, существуют также проблемы ее анализа. Дело в том, что есть вероятность того, что кто-либо из философов может так и не приступить к еде, т.к. одна из вилок или даже обе вместе могут быть постоянно заняты (так называемая ситуация "заговора" соседей[1]). А если они сядут за стол одновременно, то возникает вариант взаимной блокировки всех философов.
Структурная модель
Структурную модель задачи можно представить в виде пяти параллельных блоков. При этом в один блок удобно объединить философа и лежащую слева от него вилку. Взаимодействовать между собой блоки будут, предоставляя на время соседям свой "ресурс" - вилку. На рис. 1 представлен такой блок - "философ/вилка".
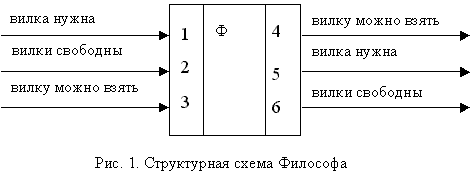
Он имеет три входных и три выходных канала. По входным каналам к блоку поступают следующие сигналы:
-
"вилка нужна" - просьба от соседа слева одолжить ему вилку;
-
"вилки свободны" - информация о том, что сосед слева данную ему вилку освободил;
-
"вилку можно взять" - разрешение от соседа справа взять его вилку.
По выходным каналам выдается информация о том, что:
-
"вилку можно взять" - сосед слева может взять запрошенную им вилку;
-
"вилка нужна" - просьба к соседу справа дать вилку;
-
"вилки свободны" - философ поел и вилки свободны (в том числе и вилка, взятая у соседа справа).
В текстовой форме структурный уровень будем отображать так:
(1,2,3)->ФN->(4,5,6)
На рис.2. представлена структурная схема соединения философов на уровне блоков.
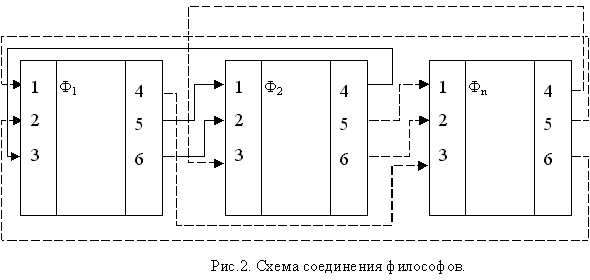
В текстовой форме эта схема будет такой:
(Ф5(5),Ф5(6),Ф2(4))->Ф1->(Ф5(3),Ф2(1),Ф2(2)),
(Ф1(5),Ф1(6),Ф3(4))->Ф2->(Ф1(3),Ф3(1),Ф3(2)),
(Ф2(5),Ф2(6),Ф2(4))->Ф3->(Ф2(3),Ф4(1),Ф4(2)),
(Ф3(5),Ф3(6),Ф3(4))->Ф4->(Ф3(3),Ф5(1),Ф5(2)),
(Ф4(5),Ф4(6),Ф4(4))->Ф5->(Ф4(3),Ф1(1),Ф1(2)).
Введем еще один уровень структурной иерархии. На нем блок "философ/вилка" состоит из блоков "вилка", "слуга" и "философ". Структурная модель вилки представлена на рис. 3. По каналам 1,2 к "ней" поступает информация от "слуги" слева о том, что ему нужна вилка и о том, что вилка освободилась. По каналам 3,4 - поступает аналогичная информация от "слуги" справа. В выходной канал 5 "вилки" выдается информация о разрешении взять вилку слуге слева, в канал 6 - справа.
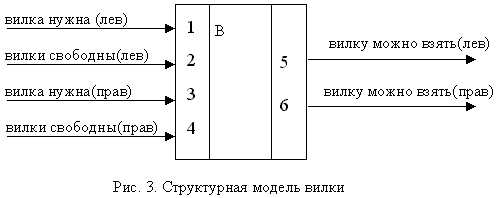
В текстовой форме структурная модель "вилки":
B: (1,2,3,4)->B->(5,6);
Структурная модель "слуги" представлена на рис. 4. По каналам 1,2 к нему поступает информация о том, что вилки свободны (соответственно вилка слева и справа), по третьему - просьба философа о еде. По 4-му выходному каналу слуга выдает запрос о том, что ему нужны вилки, по 5-му - информирует, что вилки освободились, по 6-му - предлагает философу приступить к еде.
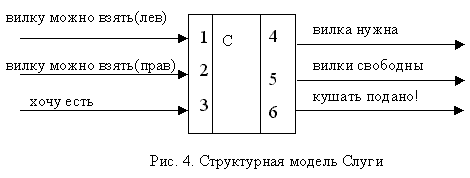
В текстовой форме:
C: (1,2,3)->C->(4,5,6),
На рис. 5. представлена общая структурная схема блока "философ/вилка" в графической форме. (В составе схемы показан и блок "фил", соответствующий философу, но его в силу его простоты далее не рассматриваем.)
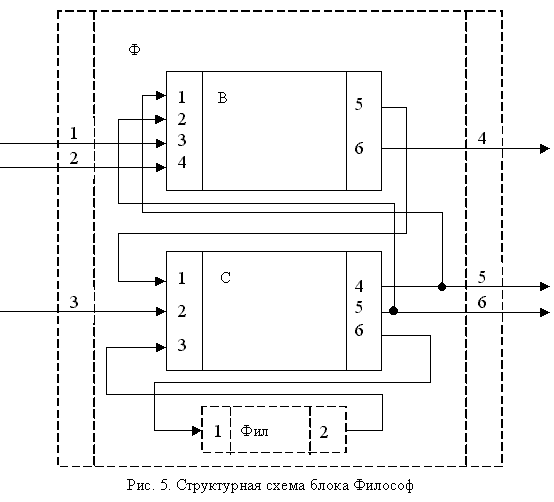
Текстовая форма структурной схемы блока "философ/вилка" с учетом внутренних и внешних связей будет выглядеть так:
ФN:
(C(4),C(5),3[1],4[2])->B->(C(1),6[4]),
(B(5),2[3],3)->C->(б(1)[5],B(2)[6],6).
Цифры в квадратных скобках содержат "имена" связей/контактов верхнего уровня. В данном случае номера контактов блока ФN. Так как из схемы исключен блок "фил", т.к. можно считать, что на вход контакта 3 блока "слуга" поступает сигнал от философа к слуге - "хочу есть", а с контакта 6 выдается сигнал "кушать подано" от слуги к философу.
Автоматная модель вилки
Приступим теперь к описанию функционирования блоков на уровне алгоритмов их работы. Для этого возьмем модель конечного автомата - для отдельного блока и сеть из автоматов на уровне параллельной работы их множества.
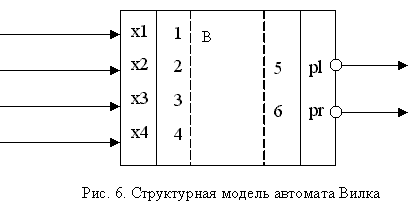
Соответствие между каналами автомата, моделирующего поведение вилки, и каналами структурной модели вилки показано на рис. 6 (кружок у выходного канала говорит о "подключении" к внутреннему состоянию автомата).
На рис. 7 приведен граф автомата P модели вилки.
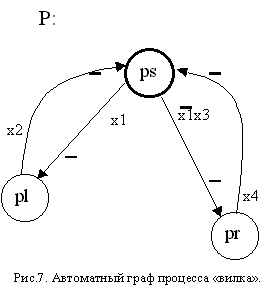
В аналитической форме его описание будет иметь следующий вид:
P: ps = {pl(x1/-), pr(^x1x3/-)}, pl = {ps(x2/-)}, pr = {ps(x4/-)}.
Где отображение каналов автоматной модели (P) на контакты ее структурной модели (В) будет следующим (см. также рис 6):
P->б: x1->1, x2->2, x3->3, x4->4, pl->5, pr->6.
Представленная выше аналитическая форма описания автоматов аналогична совершенной форме булевых функций (БФ). По ней, как и для БФ, однозначно определяется дополнение совершенного автомата до полностью определенного. В данном случае дополнение автомата P до полностью определенного автомата P' будет следующим:
^P: ps = {ps(^x1^x3/-)}, pl = {pl(^x2/-)}, pr = {pr(^x4/-)}.
Таким образом, полностью определенный автомат P', являющийся моделью структурного блока на уровне описания алгоритма его работы, определяется выражением:
P' = P 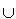 ^P (1) ^P (1)
Из него следует, что дополнение ^P до полностью определенного автомата определяется выражением:
^P = P' - P (2)
Легко видеть, что это и подобное ему автоматное дополнение состоит из множества петель автоматного графа, не имеющих выходных наборов.
У автомата, модели вилки, (см. рис. 7) в состоянии pl разрешается взять вилку левому соседу, а в pr - правому. Особенность стратегии выделения вилки состоит в том, что левому философу вилка выделяется всегда, а правому - только при отсутствии запроса от "своего" философа (безусловно, приоритеты можно поменять, но это уже будет немного другой автомат).
Аналогично автомату "Вилка" спроектирован и автомат "Слуга". На структурно уровне он показан на рис. 8, а его граф - на рис. 9.
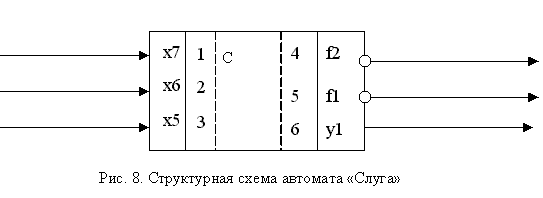
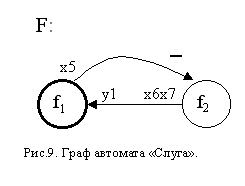
Его аналитическая форма записи имеет вид:
F: f1 = {f2(x5/-)}, f2 = {f1(x6x7/y1)}.
Где F->C: x5->3, x6->2, x7->1, f2->4, f1->5, y1->6.
Дополнение автомата ^F до автомата F' будет следующим:
^F: f1 = {f1(^x5/-)}, f2 = {f2(^x6/-), f2(^x7/-)}.
Здесь состояние f1 соответствует ситуации, когда вилки слуге (философу) не нужны или освободились после еды, а состояние f2 - состоянию запроса вилок. В состояние f2 слуга переходит при x5=1, т.е. когда философ обратится с просьбой о еде.
Сетевая автоматная модель блока "философ/вилка"
Имея модели компонент, можно создать общую модель блока "философ/вилка". Ее автоматный граф в форме автоматной сети представлен на рис. 10.
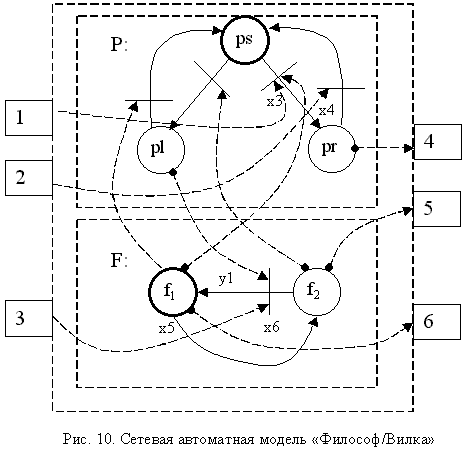
Его аналитическая форма будет выглядеть следующим образом:
P: ps = {pl(f2/-), pr(f1x3/-)}, pl = {ps(f1/-)}, pr = {ps(x4/-)}.
(3)
F: f1 = {f2(x5/-)}, f2 = {f1(plx6/y1)}.
(4)
Где x5 - сигнал "хочу есть" от философа слуге, а y1 - "можно есть" сигнал от слуги к философу.
Отображение на входные/выходные "контакты" блока ФN (напомним, что его функциональная модель - это сетевая автоматная модель M - параллельное соединение автоматов P и F, т.е. M = P||F):
x3->1, x4->2, x6->3, pr->4, f2->5, f1->6
На автоматном графе сетевой модели пунктирными стрелками отражены информационные и синхронизирующие связи компонентных автоматов сети. Для наглядного графического изображения синхронизации введен элемент "полочка", аналогичный "полочке" в сетях Петри. В аналитической форме синхронизирующая информация отражается через имена состояний автоматов, которые соответствуют входным переменным компонентных автоматов. Например, переменной x1 соответствует состояние f2, ^x1 - f1 и т.д. (см. также структурные схемы автоматов рис. 6, 8)
Для построения эквивалентного автомата нам понадобятся дополнения компонентных автоматов сети, которые в этом случае будут следующими:
^P: ps = {ps(f1^x3/-)}, pl = {pl(f2/-)}, pr = {pr(^x4/-)}.
^F: f1 = {f1(^x5/-)}, f2 = { f2(pr/-), f2(ps/-), f2(^x6/-)}.
Сеть реализует некий общий алгоритм, который может быть представлен автоматом, эквивалентным рассматриваемому множеству параллельно функционирующих автоматов. Для описания системы сетевое представление предпочтительнее, т.к. в большинстве случаев оно гораздо компактнее эквивалентной формы. Его и составить проще, формируя компонентные автоматы, в сравнении с определением алгоритма поведение системы "одним куском". В то же время по эквивалентному автомату гораздо точнее можно судить о поведении системы. Покажем это на примере нахождения эквивалентного данной сетевой модели автомата
Автомат эквивалентный сетевой модели "философ/вилка"
Пусть нам даны два автомата P и F. Автомат M, эквивалентный параллельной работе двух автоматов, определяется выражением:
M = P 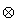 F = P F = P 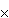 ^F ^F 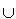 ^P ^P 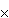 F F 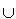 P P 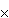 F,
(5) F,
(5)
где 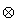 - операция алгебраического "параллельного" умножения автоматов. Об определении алгебраических операциях над автоматами (правда, абстрактными, а у нас - структурные) см. [3]. Используя совершенные формы автоматов и их дополнений, найдем элементы, составляющие формулу (5): - операция алгебраического "параллельного" умножения автоматов. Об определении алгебраических операциях над автоматами (правда, абстрактными, а у нас - структурные) см. [3]. Используя совершенные формы автоматов и их дополнений, найдем элементы, составляющие формулу (5):
P 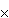 ^F: ^F:
psf1 = {prf1(x3^x5/-)}, psf2 = { plf2(-/-)},
plf1 = {psf1(^x5/-)}, plf2 = {-},
prf1 = {psf1(x4^x5/-)}, prf2 = {psf2(x4/-)}.
^P 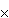 F: F:
psf1 = {prf2(x3x5/-)}, psf2 = {-},
plf1 = {psf2(x5/-)}, plf2 = {-},
prf1 = {psf2(x4x5/-)}, prf2 = {-}.
P 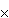 F: F:
psf1 = {prf2(x3x5/-)}, psf2 = {-},
plf1 = {psf2(x5/-)}, plf2 = {-},
prf1 = {psf2(x4x5/-)}, prf2 = {-}.
Окончательно:
P 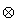 F = P F = P 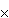 ^F ^F 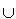 ^P ^P 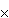 F F 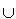 P P 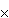 F: F:
psf1 = {prf1(x3^x5/-), psf2(^x3x5/-), prf2(x3x5/-)},
psf2 = {plf2(-/-)},
plf1 = {psf1(^x5/-), psf2(x5/-) },
plf2 = {plf1(x6/y1)},
prf1 = {psf1(x4^x5/-), prf2(^x4x5/-), psf2(x4x5/-)},
prf2 = {psf2(x4/-)}.
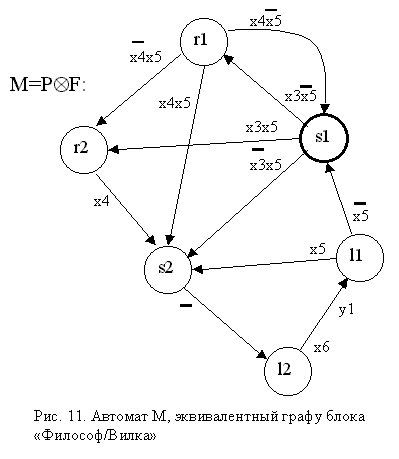
Графическая форма эквивалентного автомата представлена на рис.11. На ней имена состояний эквивалентного автомата составлены из символов компонентных автоматов сети.
Анализ поведения философа
Эквивалентная однокомпонентная модель детально отражает поведение системы "вилка-слуга-философ" в целом. Глядя на рис. 11, можно, например, обратить внимание на цикл, образуемый состояниями s2-l2-l1-s2. Автомат будет "циклиться", если при переходе из состояния l2 в состоянии l1 переменная x5 ("хочу есть") будет иметь истинное значение. Это соответствует примеру голодного философа, который, поев на переходе l2-l1, тут же изъявляет желание снова есть.
Маловероятно, конечно, что философ поглотит еду за один автоматный такт, но в данном случае "скорость" еды определяется предполагаемой внешней моделью философа, которая может иметь, например, и такой простой вид:
D: d1 = {d2(-/y1)}, d2 = {d1(-/y2)}.
Здесь действие y1 устанавливает переменную, соответствующую сигналу x5, в ноль, а y2 - устанавливает ее в единицу, т.е. в значение "хочу есть".
Кроме ситуации зацикливания модель показывает и вероятность возникновения тупика. Это случится, когда все автоматы из своего начального состояния s1 (при х5=1) за пару "скачков" (дискретных тактов) одновременно попадут в состояние l2, где зависнут (при x6=0), т.к. не будет предоставлена вилка соседом справа. Однако тупика не будет, если хотя бы один из автоматов не получит сигнал "хочу есть". Тогда он, находясь в состоянии s1, даст соседу вилку (x3=1), перейдя в состояние r1.
Кстати, философ может зависнуть и в r1 в том случае, если по каким-то причинам сосед ему вилку не вернет. В реальной жизни такое случается, но в нашей модели, сосед, взяв вилку, не вернуть ее уже не может. Во-первых, потому, что он отдаст свою вилку только в том случае, если она ему самому не нужна (см. переход в состояние pr на рис. 8), а, отдав вилку, уже не будет ее просить у нас, т.к. будет ждать возврата вилки. Во-вторых, если его вилка свободна, а он хочет есть, то его компонента "вилка" перейдет в состояние pl, заняв тем самым свою вилку, а его слуга перейдет в состояние f2 - запроса вилки у своего соседа, т.е. у нас. Таким образом, сосед будет требовать у нас вилку только в том случае, если он уже "застолбил" свою. А потому, дав ему вилку, мы в праве дождаться ее возвращения, т.к. соседу условия для поглощения пищи предоставлены, а поев, он уж обязательно должен вилки освободить.
Более сложная модель блока "философ/вилка" представлена на рис. 12. В ней каждому философу выделена тарелка (автомат Q), введена в явной форме и модель философа (автомат D). Кроме того, с учетом новых моделей и взаимодействия с ними и между ними изменена модель слуги (автомат F). При этом автомат "вилка" и состав связей с внешней средой на уровне блока "философ/вилка" остались неизменными. Можно видеть, что уже просто по числу внутренних состояний граф, эквивалентный сетевой модели на рис. 12, будет сложнее графа на рис. 11. Если у графа на рис. 11 их всего шесть, то для графа на рис.12 их будет 72 (определяется произведением состояний компонентных автоматов сети).
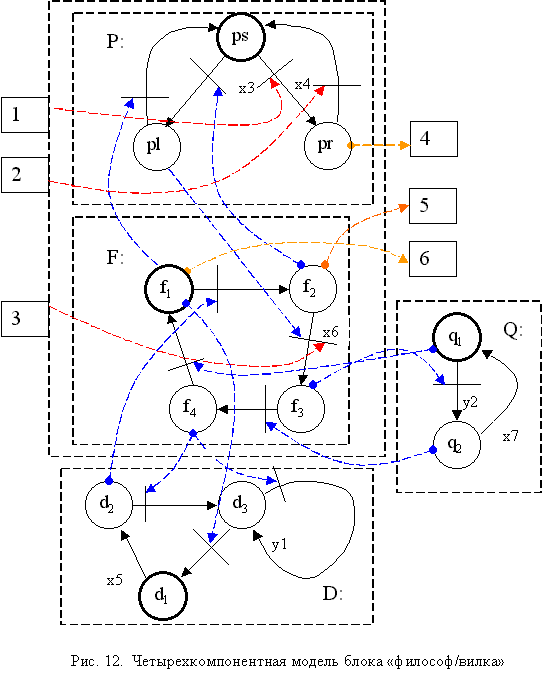
f1 - вилки свободны
f2 - нужны вилки
f3 - вилки выданы
f4 - можно есть
q1 - тарелка пуста
q2 - тарелка наполнена
y2 - наполнить тарелку
d1 - философ сыт
d2 - голоден
d3 - ест
y1 - съесть часть порции макарон
Об устранение тупика
Для исключения тупика можно ввести дополнительный блок, который не будет допускать к столу всех философов одновременно. В этом случае все запросы о еде должны им фильтроваться. Если запросов поступит столько, сколько философов, то любой из запросов нужно задержать хотя бы на один такт автоматного времени. В остальных случаях все запросы пропускаются без задержки. В реальной жизни таким блоком может быть автоматика открывания дверей, через которые философы входят в столовую.
Выводы
Известно множество разных решений данной задачи. Но есть у них одно общее - параллелизм формальных моделей, на базе которых они получены. Из этих моделей, возможно, самые популярные сети Петри (см. например, [1]). Примером решения на базе другой модели служит решение, рассмотренное в [2]. Хочется надеяться, что приведенное нами автоматное решение столь известной задачи позволит с иных позиций взглянуть и на проблемы реализации параллельных систем вообще и на вопросы применения автоматов для описания и реализации их параллелизма в частности.
Обычно понятие конечного автомата связывается только с последовательными процессами и отвергается при переходе к параллельным системам. Действительно, отдельный автомат больше приспособлен для описания одного процесса (хотя и на этом уровне у него есть возможности для задания параллелизма). Но уже множество автоматов, представленное на формальном уровне автоматной сетью, моделирует системы параллельного типа не хуже, чем специально разработанные для таких систем модели (например, те же сети Петри).
Литература
-
Элементы параллельного программирования/В.А. Вальковский, В.Е. Котов, А.Г. Марчук, Н.Н. Миренков; Под ред. В.Е. Котова. - М.: Радио и связь, 1983. - 240с.
-
Хоар Ч. Взаимодействующие последовательные процессы: Пер. с англ. - М.: Мир, 1989. 264 с.
-
Мелихов А.Н. Ориентированные графы и конечные автоматы. - М.: Наука, 1971. - 416 с.
|