|
©1983
Вячеслав Любченко
|
|
Тот, кто знает и не знает, что он не знает,
- глупец, избегай его.
Тот, кто не знает и знает, что он не знает,
может научиться, научи его.
Тот, кто знает и не знает, что он знает,
спит, разбуди его.
Тот, кто знает и знает, что он знает,
- пророк, учись у него.
Древнее персидское стихотворение
(по кн. Э.Хамби. Программирование таблиц решений).
|
В последнее время в связи с распространением идей структурного программирования большую популярность приобретают табличные способы задания алгоритмов [1]. Применение так называемых таблиц решений (ТР) позволяет просто, ясно и компактно описывать задачи на языке, понятном широкому кругу специалистов [2]. Однако, несмотря на ряд достоинств, применение ТР носит недостаточно широкий характер. Связано это с невозможностью описания с помощью "чистых" таблиц решений алгоритмов, содержащих циклические конструкции.
Целью данной работы является описание формальной модели программ, обладающей преимуществами, присущими ТР, и применимой для описания алгоритмов любой структуры. Предложенная модель принадлежит к классу автоматных моделей. Теоретической базой для автоматного подхода к заданию алгоритмов является теория конечных автоматов и теория вычислимых функций по Тьюрингу [3].
В общем случае программа может быть представлена как конечное множество операторов над памятью, для которых задан порядок выполнения. Формальная математическая модель программы тогда может быть представлена схемой программы, определяемой как тройка S = (M, A, G) [4]. Здесь M - множество ячеек памяти, A - множество операторов программы, которые в свою очередь могут быть программами, G - управление.
Во множестве A выделим операторы логического типа (предикаты) xi 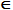 X и операторы функционального типа (действия) yi X и операторы функционального типа (действия) yi 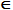 Y, т.е. A = (X,Y), где X = {xi}, Y = {yi} и X Y, т.е. A = (X,Y), где X = {xi}, Y = {yi} и X 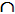 Y = 0, |A| = |X| + |Y|. Каждому оператору из A ставится в соответствие множество входных ячеек памяти Da Y = 0, |A| = |X| + |Y|. Каждому оператору из A ставится в соответствие множество входных ячеек памяти Da 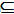 M. Множество выходных ячеек Ra M. Множество выходных ячеек Ra 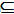 M определено только для операторов функционального типа yi M определено только для операторов функционального типа yi 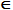 Y. Значением логического оператора xi Y. Значением логического оператора xi 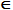 X является константа 0, если вычисленное им условие ложно, и 1, если истинно. Таким образом, с помощью действий осуществляются необходимые преобразования над множеством ячеек памяти, а с помощью предикатов анализируются возникающие при этом ситуации. X является константа 0, если вычисленное им условие ложно, и 1, если истинно. Таким образом, с помощью действий осуществляются необходимые преобразования над множеством ячеек памяти, а с помощью предикатов анализируются возникающие при этом ситуации.
Работу управления по анализу ситуаций и управлению действиями удобно описывать в терминах некоторой абстрактной машины с конечным числом состояний. Формальной математической моделью такой машины является модель конечного автомата [5]. Абстрактный конечный автомат - это кортеж или вектор S = (Q, Z, W, 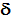 , , 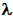 , q0), у которого , q0), у которого
-
Q = {q0, q1, ... qk} - множество состояний;
-
Z = { z0, z1, ... zk } - множество входных сигнале;
-
W = { w0, w1, ... wl } - множество выходных сигналов;
-
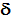 : Q : Q 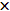 Z Z 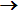 Q - функция переходов; Q - функция переходов;
-
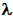 : Q : Q 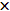 Z Z 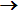 Y - функция выходов; Y - функция выходов;
-
q0 - начальное состояние.
Если функции 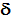 и и 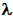 заданы на всем множестве Q заданы на всем множестве Q 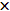 Z, то автомат называется полностью определенным, в противном случае - частичным. В зависимости от вида функций Z, то автомат называется полностью определенным, в противном случае - частичным. В зависимости от вида функций 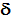 и и 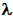 выделяют два основных типа (рода) автоматов: автоматы Мили и автоматы Мура. Закон функционирования используемой далее модели автомата Мили задается уравнениями: выделяют два основных типа (рода) автоматов: автоматы Мили и автоматы Мура. Закон функционирования используемой далее модели автомата Мили задается уравнениями:
q(t+1) = 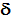 (q(t), z(t)), (q(t), z(t)),
w(t) = 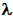 (q(t), z(t)). (q(t), z(t)).
Для более подробного описания объекта моделирования (программы) необходимо перейти от абстрактного автомата S к структурному автомату G [5]. В структурном автомате G учитывается структура входных и выходных сигналов, определяемых уже как входные и выходные наборы автомата.
Структура наборов зависит от множества операторов из А. Входным наборам соответствуют ситуации программы, а выходные наборы определяют последовательность выполнения действий. Причем, если значение предиката xi в конкретной ситуации должно быть истинным, то это обозначается как xi, в противном случае - ~xi.
Из существующих способов описания автоматов наиболее часто применяемыми являются табличный и графический, В качестве табличного способа описания будем использовать сокращенную форму прямых структурных таблиц переходов автомата (в дальнейшем просто таблиц переходов) [5]. Графическим средством изображения конечных автоматов являются нагруженные ориентированные графы. Каждая вершина графа отождествляется с некоторым состоянием автомата, а дуги - с парами букв входного и выходного наборов. Состояния автомата записывают внутри кружков, соответствующих вершинам графа, входной и выходной наборы указывают над соответствующей дугой. Пример графа частичного (о чем говорят прочерки над дугами) автомата Мили приведен на рис. 1.
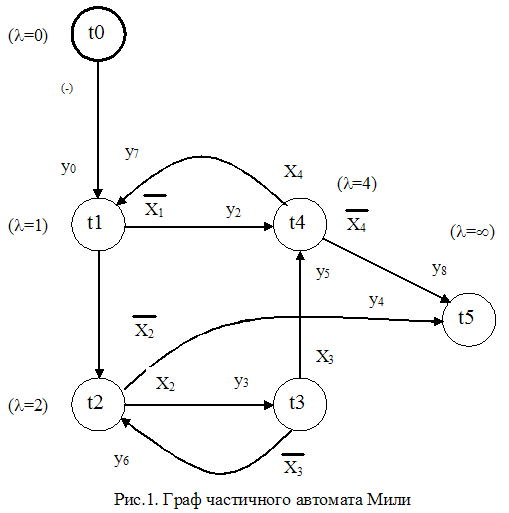
Поскольку целью работы является демонстрация преимущества автоматного подхода по сравнению с ТР, примеры, приведенные далее, взяты из опубликованных работ по таблицам решений.
Рассмотрим пример, взятый из [6]. Основным результатом работы [6] является доказательство существования для любой блок-схемы программы эмулирующей ее повторновходимой таблицей решений. Для достижения поставленной цели в ТР вводится специальная переменная 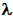 , принимающая целые положительные значения. Блок-схема программы примера из [6] представлена на рис. 2, , принимающая целые положительные значения. Блок-схема программы примера из [6] представлена на рис. 2,
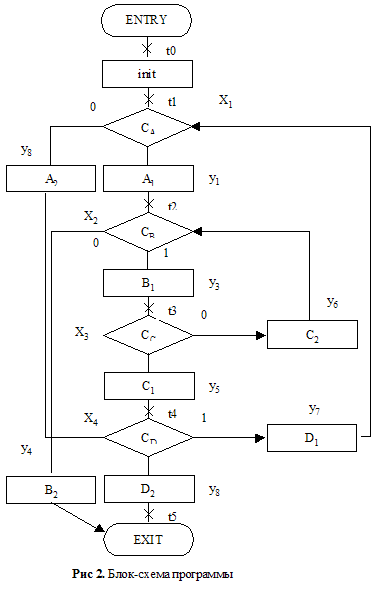
соответствующая ей ТР в табл. 1. Однако, как нетрудно заметить, предложенный прием не является новым, т.к. аналогичен способу перевода неструктурированных программ в структурированные, предложенному Ашкрофтом и Манной. Переменной 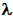 соответствует переменная I в методе Ашкрофта-Манны [1]. От табл. 1 просто перейти к частичному автомату Мили, граф которого приведен на рис. 1. В этом случае различным значениям переменной соответствует переменная I в методе Ашкрофта-Манны [1]. От табл. 1 просто перейти к частичному автомату Мили, граф которого приведен на рис. 1. В этом случае различным значениям переменной 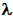 ставятся в соответствие состояния автомата. ставятся в соответствие состояния автомата.
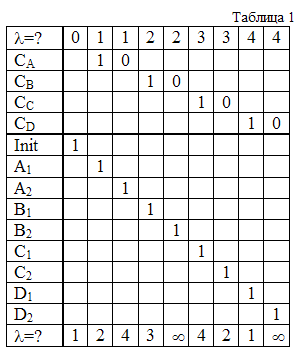
Таким образом, на примере из [6] можно видеть, что попытки обобщить ТР приводят лишь к табличной форме задания конечных автоматов. Дополнительным фактом, говорящим в пользу этого утверждения, является существование метода перехода от граф-схем алгоритмов (ГСА) к автоматному описанию дискретных устройств, предложенного в [5]. Переменной 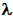 в этом случае соответствуют отметки ГСА. в этом случае соответствуют отметки ГСА.
Рассмотрим пример из [7]. Здесь поставлена следующая задача: разработать алгоритм обработки результатов слежения за значением некоторого технологического параметра. Исходными данными являются значения параметра r, текущее значение времени t, значение верхнего rв и нижнего rн пределов.
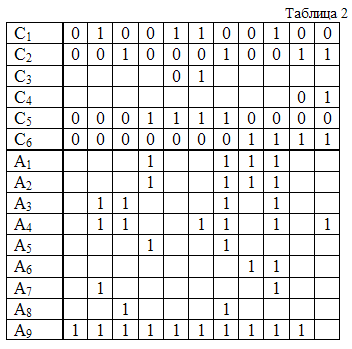
Алгоритм в виде ТР представлен табл. 2, где С1, С2, ... С6 - предикаты, A1, A2, ... A9 - действия и С1 - r > rв; С1 - r < rн; С3 - r > rэ; С4 - r < rэ; С5 - признак выхода параметра за верхний предел, С6 - признак выхода значения параметра за нижний предел; A1 - t2 := t; A2 - оператор "Выдать запись"; A4 - rэ := r; A5 - C5 := 0; A6 - C6 := 0; A7 - C5 := 1; A8 - C6 := 0; A9 - оператор "Перейти к следующему измерению".
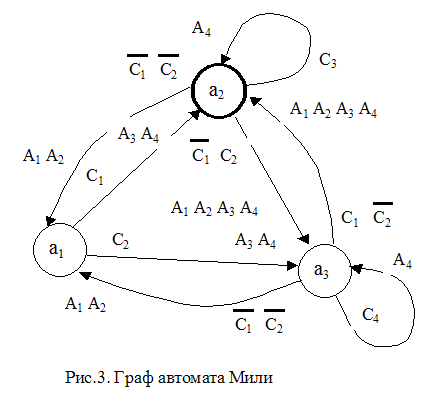
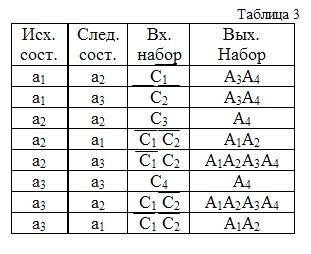
На рис. 3 и в табл. 3 представлены граф и таблица переходов автомата, реализующего ту же задачу. В результате множество операторов программы A = (X,Y), где X = { C1, C2, C3, C4}, Y = { A1, A2, A3, A4} сократилось с 15 до 8, количество решений (дуг) также уменьшилось Переменным C5, C6 из ТР стали соответствовать состояния a2,a3 автомата.
Автором данной статьи реализована и применена в практических разработках описанная выше автоматная модель программ. Для этого разработан макроязык на базе ЭВМ СМ-4, обеспечивающий программиста средствами для описания автоматов, представленных таблицами переходов. Дополнительно были разработаны средства отладки, позволяющие трассировать переменную состояния программы. Следует также отметить, что процесс проектирования при автоматном подходе, носит более строгий характер, т.к. опирается на эффективный аппарат теории конечных автоматов.
Литература
Иодан Э. Структурное проектирование и конструирование программ. - М.: Мир, 1979 - 415 с.
Фрайтаг Г., Годе В., Якоби X. и др. Введение в технику работы с таблицами решений. - М.: Энергия, 1979
-88 с.
Трахтенброт А.Б. Алгоритмы и вычислительные автоматы. - М.: Сов. радио, 1974-200 с.
Карп P.M., Миллер Р.Е. Параллельные схемы программ. - В кн. Кибернетический сборник (новая сер.). М.: Мир, 1975, вып. 13, с. 5-61.
Баранов С.И. Синтез микропрограммных автоматов. - Л.: Энергия, 1979 -232 с.
Lew A. On the emulation of flowcharts by decision tables/ - Commun. ACM, 1982, 25, №12, p. 895-905, Серия Э.И. "Вычислительная техника". - М.: ВИНИТИ, 1983, №32, с. 15-19.
Букин В.В., Жуковский В.Г. Об использовании формализованных спецификаций технологических программ систем управления. - УСиМ, 1983, №3, с. 43-47.
|